Skip to contents

Random Effect Covariances

2024-09-18

Source: vignettes/addingCovariances.Rmd
addingCovariances.Rmd
nlmixr
nlmixr

Adding Covariances between random effects

You can simply add co-variances between two random effects by adding the effects together in the model specification block, that is eta.cl+eta.v ~. After that statement, you specify the lower triangular matrix of the fit with c().

An example of this is the phenobarbitol data:

## Load phenobarbitol data
library(nlmixr2)

Model Specification 

pheno <- function() {
  ini({
    tcl <- log(0.008) # typical value of clearance
    tv <-  log(0.6)   # typical value of volume
    ## var(eta.cl)
    eta.cl + eta.v ~ c(1, 
                       0.01, 1) ## cov(eta.cl, eta.v), var(eta.v)
                      # interindividual variability on clearance and volume
    add.err <- 0.1    # residual variability
  })
  model({
    cl <- exp(tcl + eta.cl) # individual value of clearance
    v <- exp(tv + eta.v)    # individual value of volume
    ke <- cl / v            # elimination rate constant
    d/dt(A1) = - ke * A1    # model differential equation
    cp = A1 / v             # concentration in plasma
    cp ~ add(add.err)       # define error model
  })
}

Fit with SAEM 

fit <- nlmixr(pheno, pheno_sd, "saem",
              control=list(print=0), 
              table=list(cwres=TRUE, npde=TRUE))
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00

print(fit)
#> ── nlmixr² SAEM OBJF by FOCEi approximation ──
#> 
#>           OBJF      AIC      BIC Log-likelihood Condition#(Cov) Condition#(Cor)
#> FOCEi 689.3203 986.1912 1004.452      -487.0956        6.033342        5.252589
#> 
#> ── Time (sec $time): ──
#> 
#>            setup optimize covariance   saem table compress
#> elapsed 0.003707    6e-06   0.019007 12.111 3.384    0.024
#> 
#> ── Population Parameters ($parFixed or $parFixedDf): ──
#> 
#>          Est.     SE %RSE    Back-transformed(95%CI) BSV(CV%) Shrink(SD)%
#> tcl     -5.02  0.075  1.5 0.00663 (0.00573, 0.00769)     51.8      3.26% 
#> tv       0.35 0.0548 15.7          1.42 (1.27, 1.58)     41.9      1.40% 
#> add.err  2.76                                   2.76                     
#>  
#>   Covariance Type ($covMethod): linFim
#>   Correlations in between subject variability (BSV) matrix:
#>     cor:eta.v,eta.cl 
#>           0.946  
#>  
#> 
#>   Full BSV covariance ($omega) or correlation ($omegaR; diagonals=SDs) 
#>   Distribution stats (mean/skewness/kurtosis/p-value) available in $shrink 
#>   Censoring ($censInformation): No censoring
#> 
#> ── Fit Data (object is a modified tibble): ──
#> # A tibble: 155 × 26
#>   ID     TIME    DV EPRED  ERES   NPDE     NPD   PDE    PD  PRED    RES    WRES
#>   <fct> <dbl> <dbl> <dbl> <dbl>  <dbl>   <dbl> <dbl> <dbl> <dbl>  <dbl>   <dbl>
#> 1 1        2   17.3  18.9 -1.58 -0.350 -0.0920 0.363 0.463  17.5 -0.162 -0.0214
#> 2 1      112.  31    29.7  1.25  0.245  0.245  0.597 0.597  28.0  2.98   0.244 
#> 3 2        2    9.7  11.4 -1.71 -0.664 -0.202  0.253 0.42   10.5 -0.777 -0.154 
#> # ℹ 152 more rows
#> # ℹ 14 more variables: IPRED <dbl>, IRES <dbl>, IWRES <dbl>, CPRED <dbl>,
#> #   CRES <dbl>, CWRES <dbl>, eta.cl <dbl>, eta.v <dbl>, A1 <dbl>, cl <dbl>,
#> #   v <dbl>, ke <dbl>, tad <dbl>, dosenum <dbl>

Basic Goodness of Fit Plots 

plot(fit)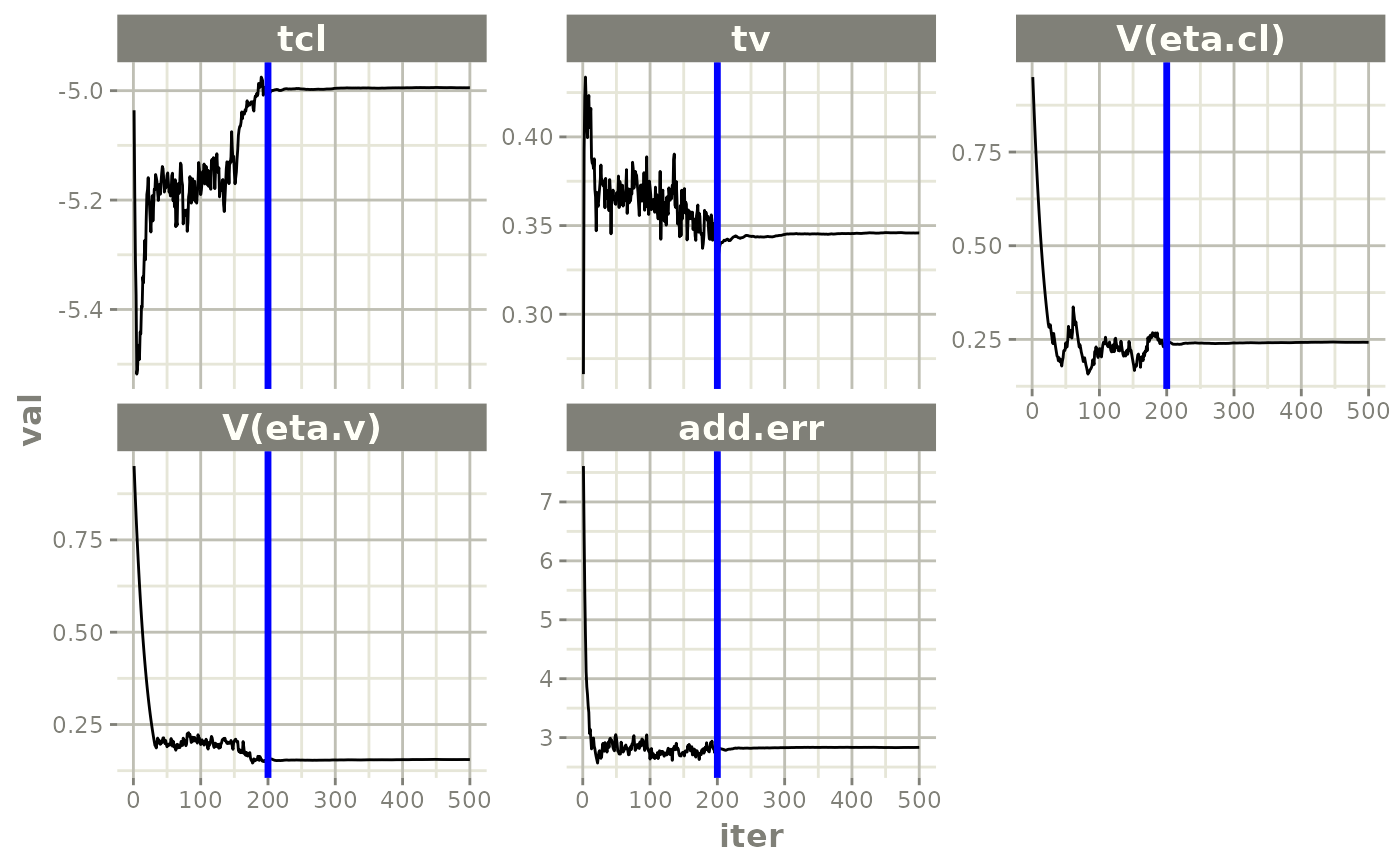

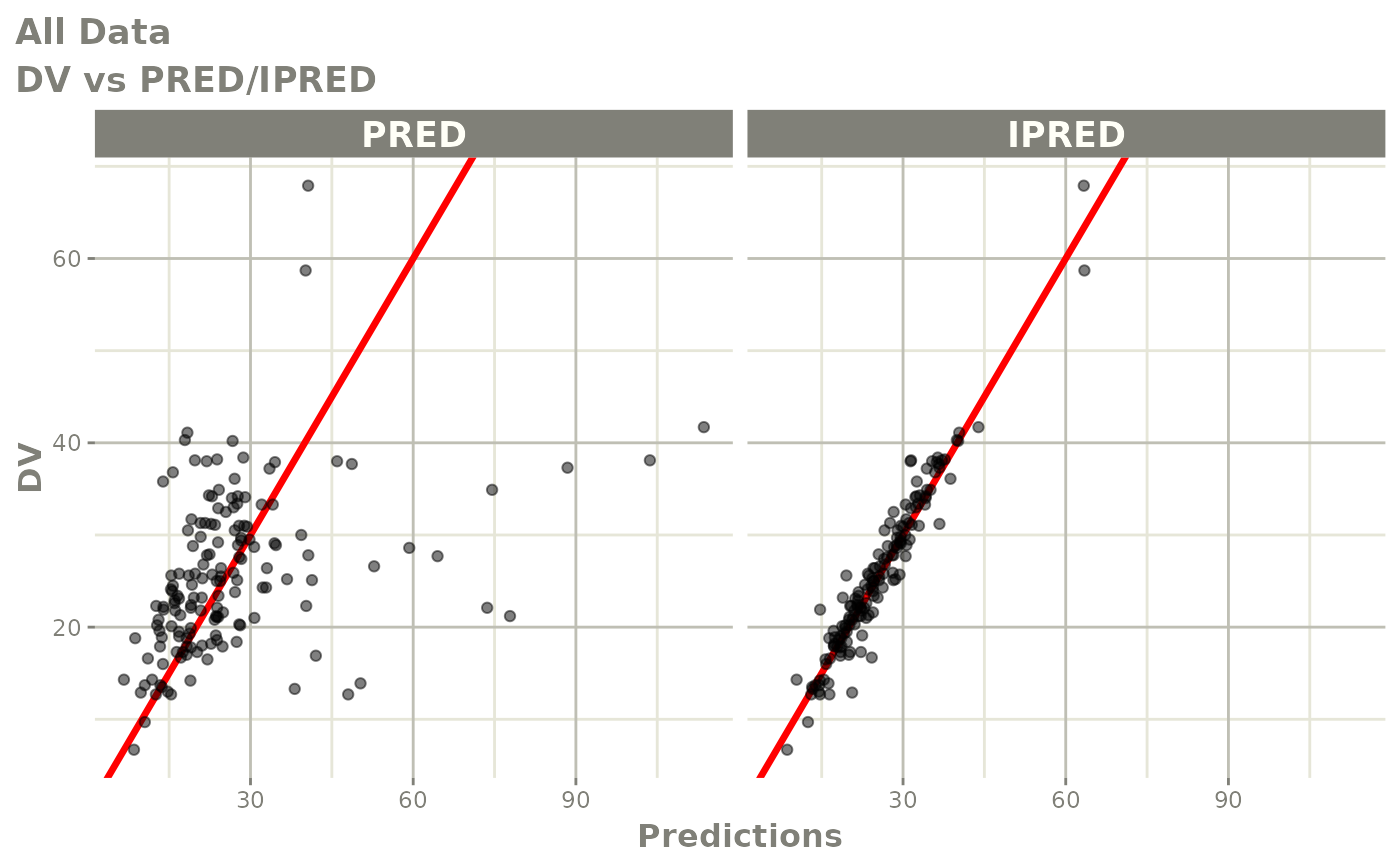
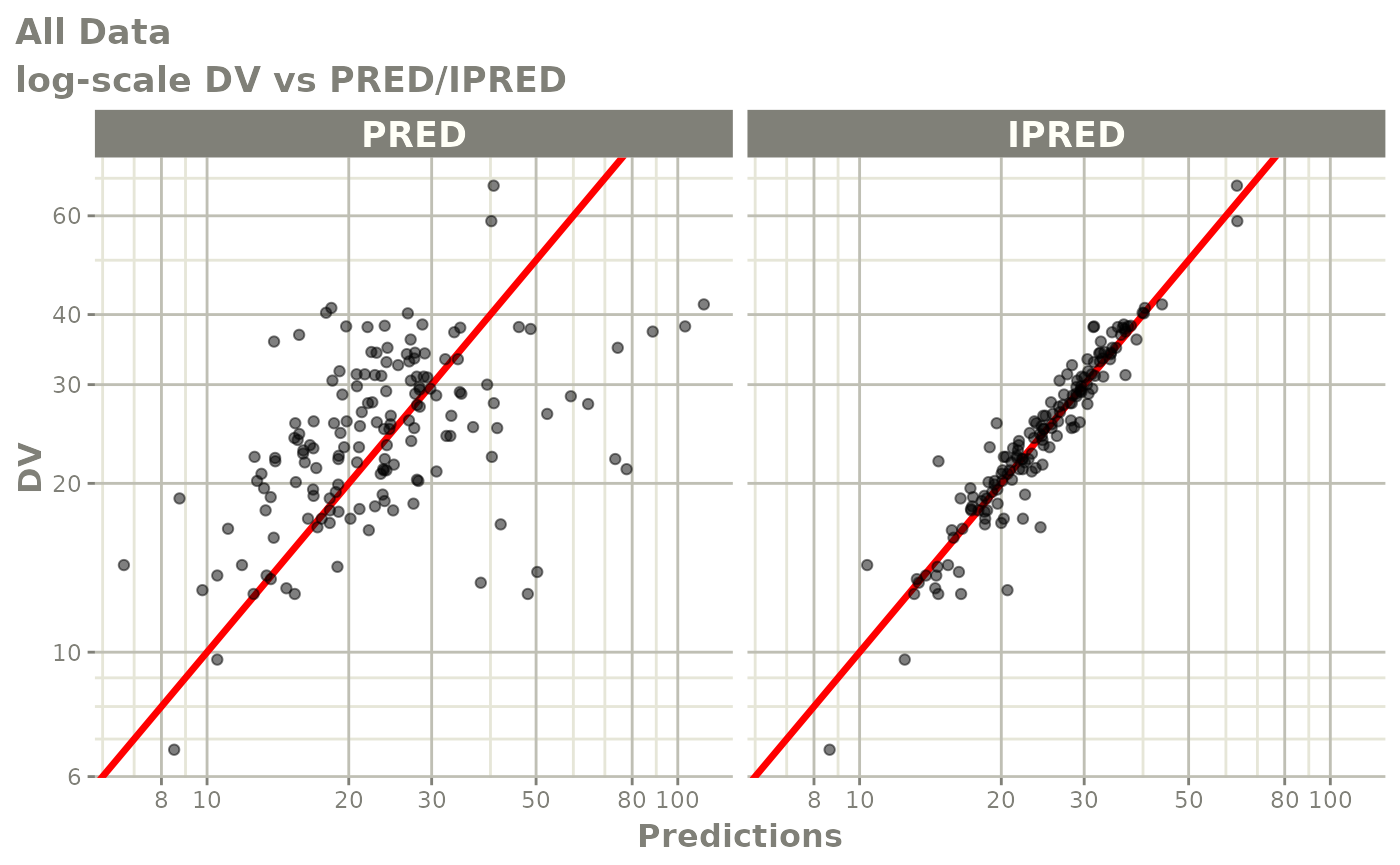
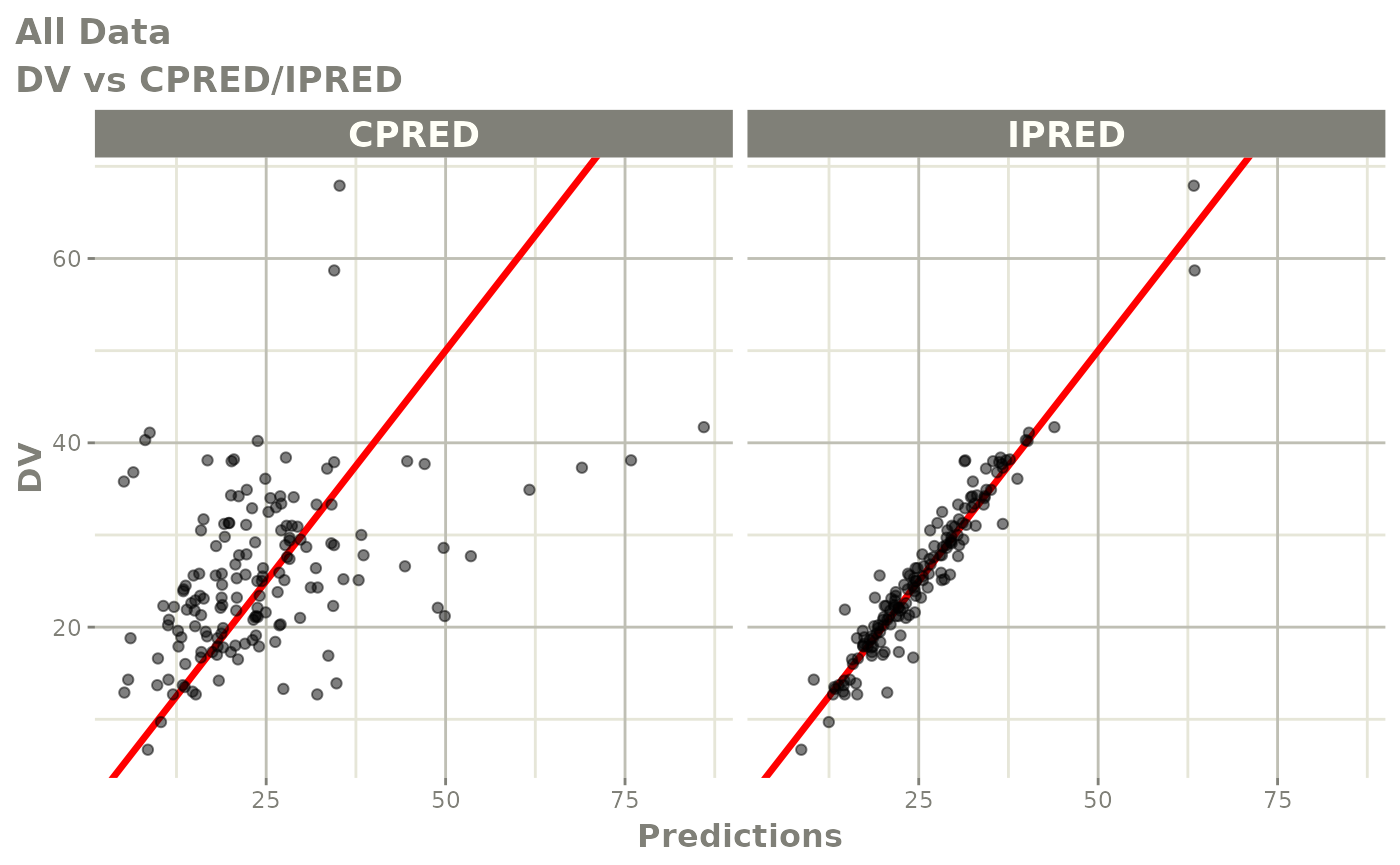
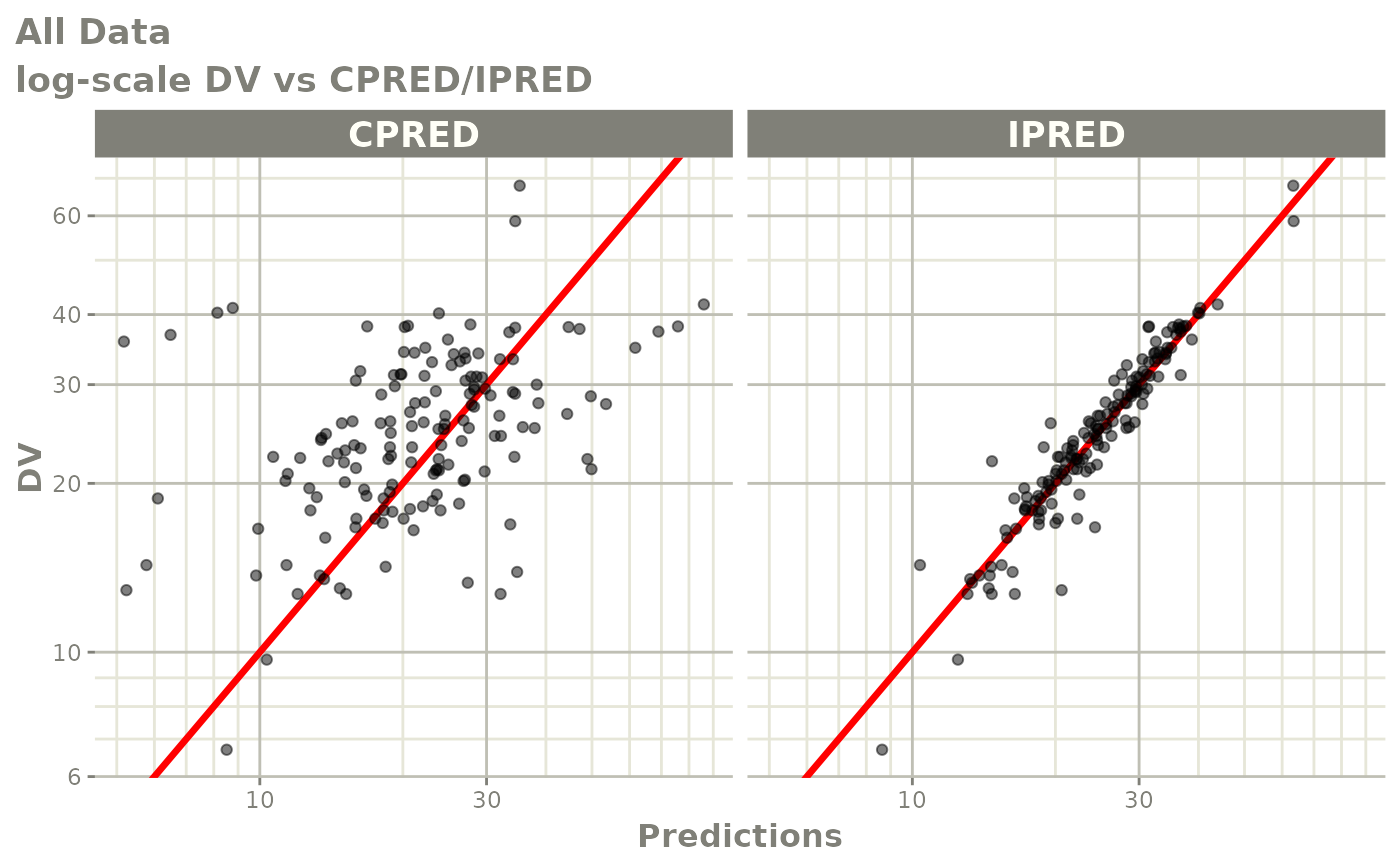
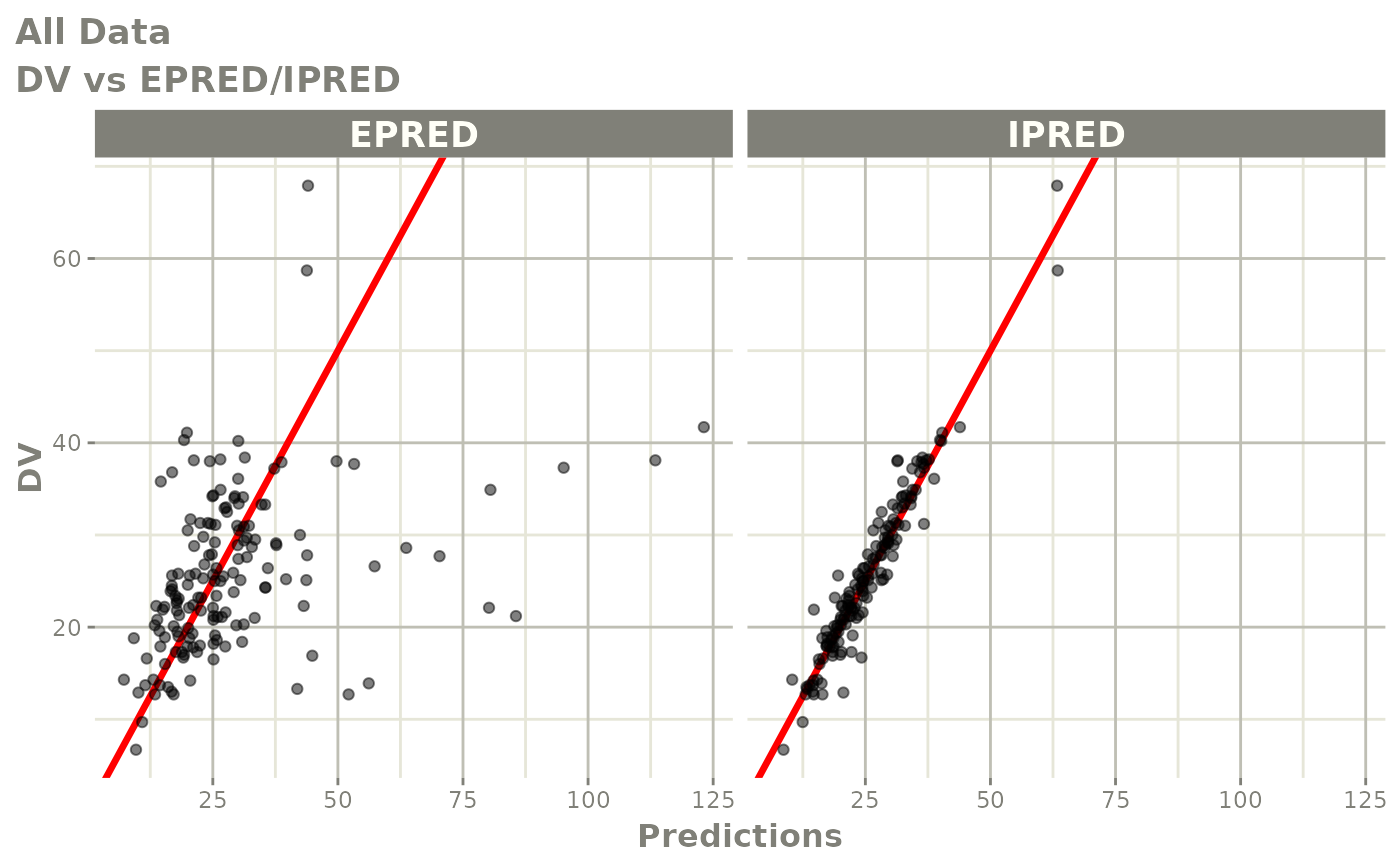
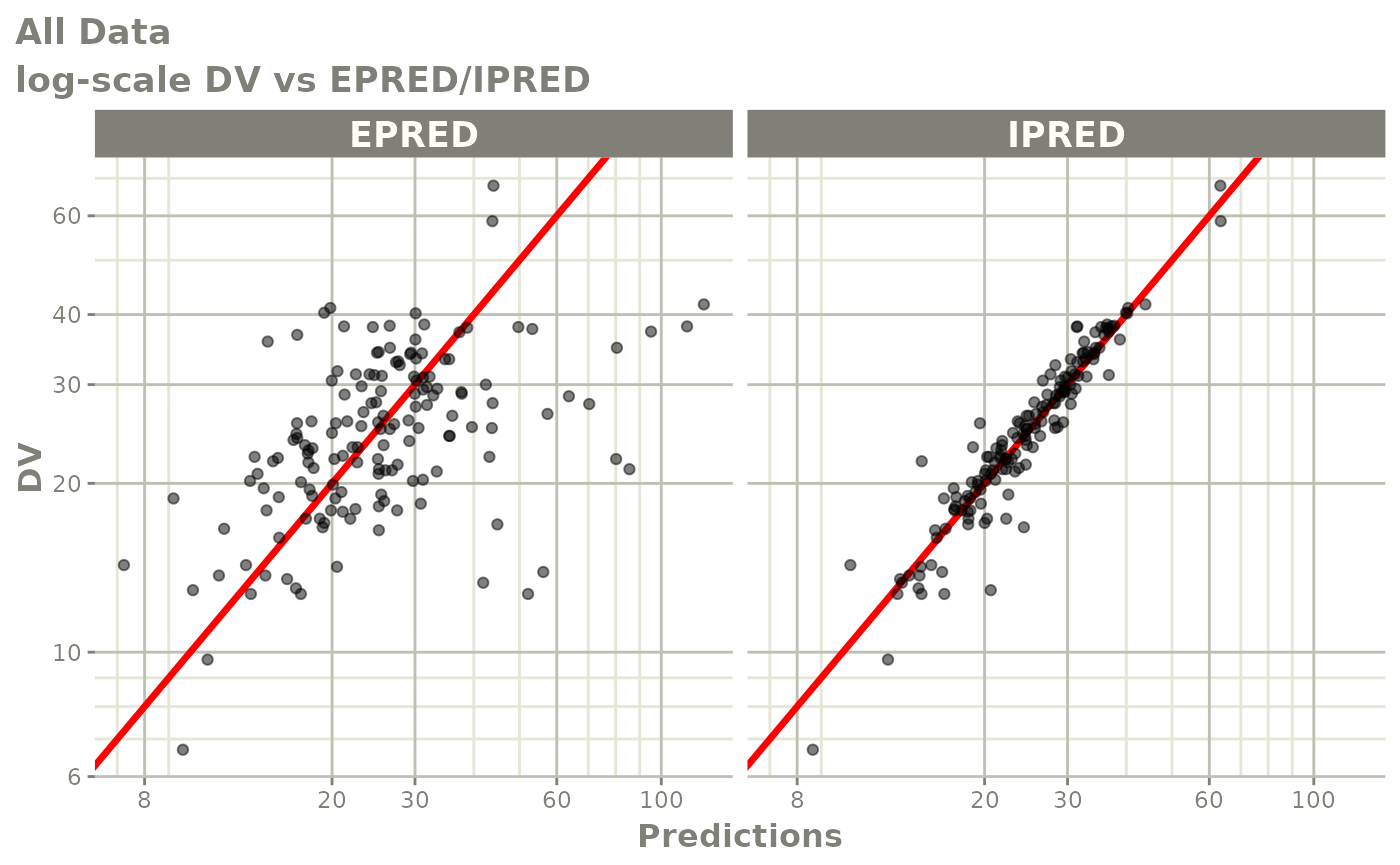
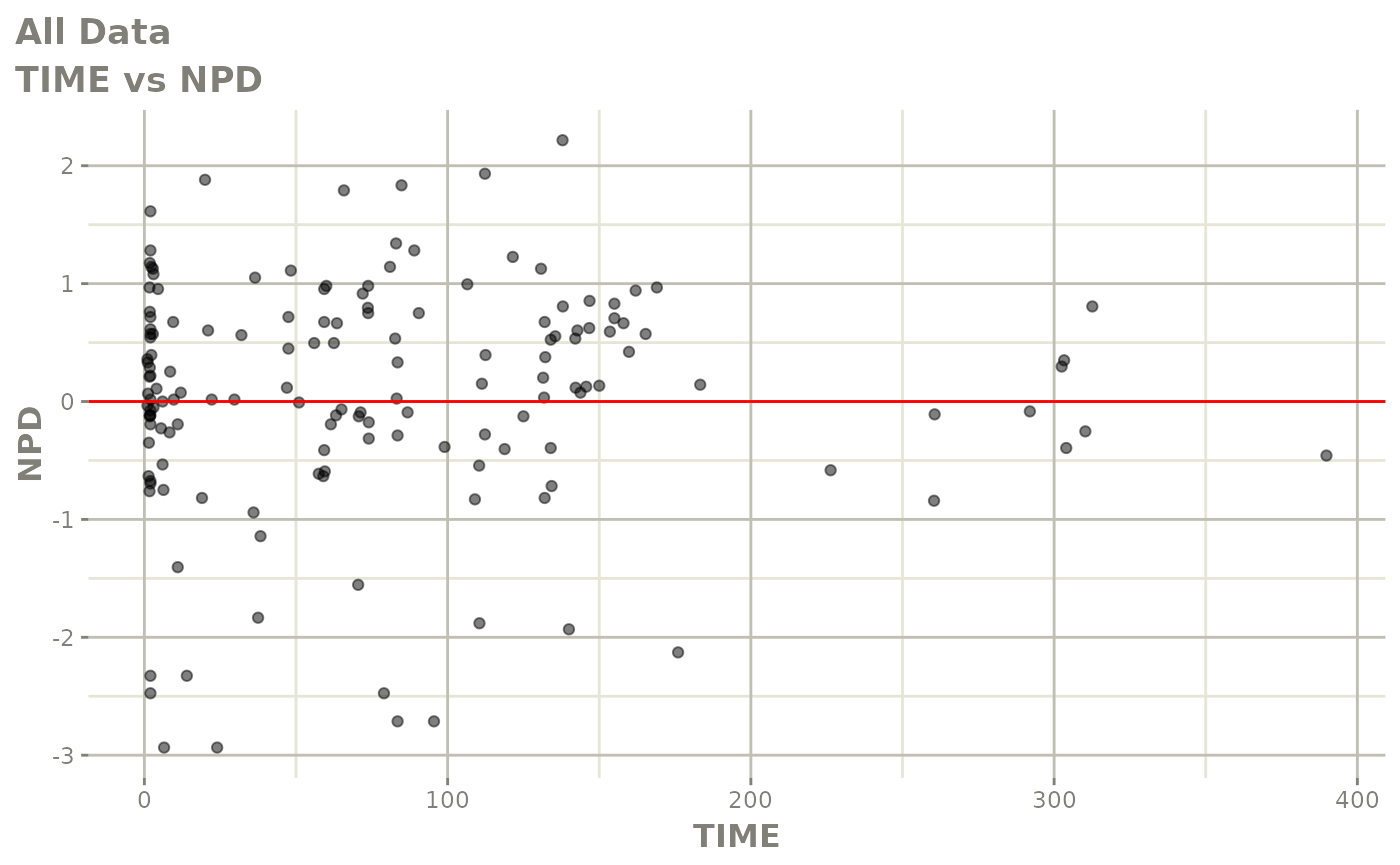
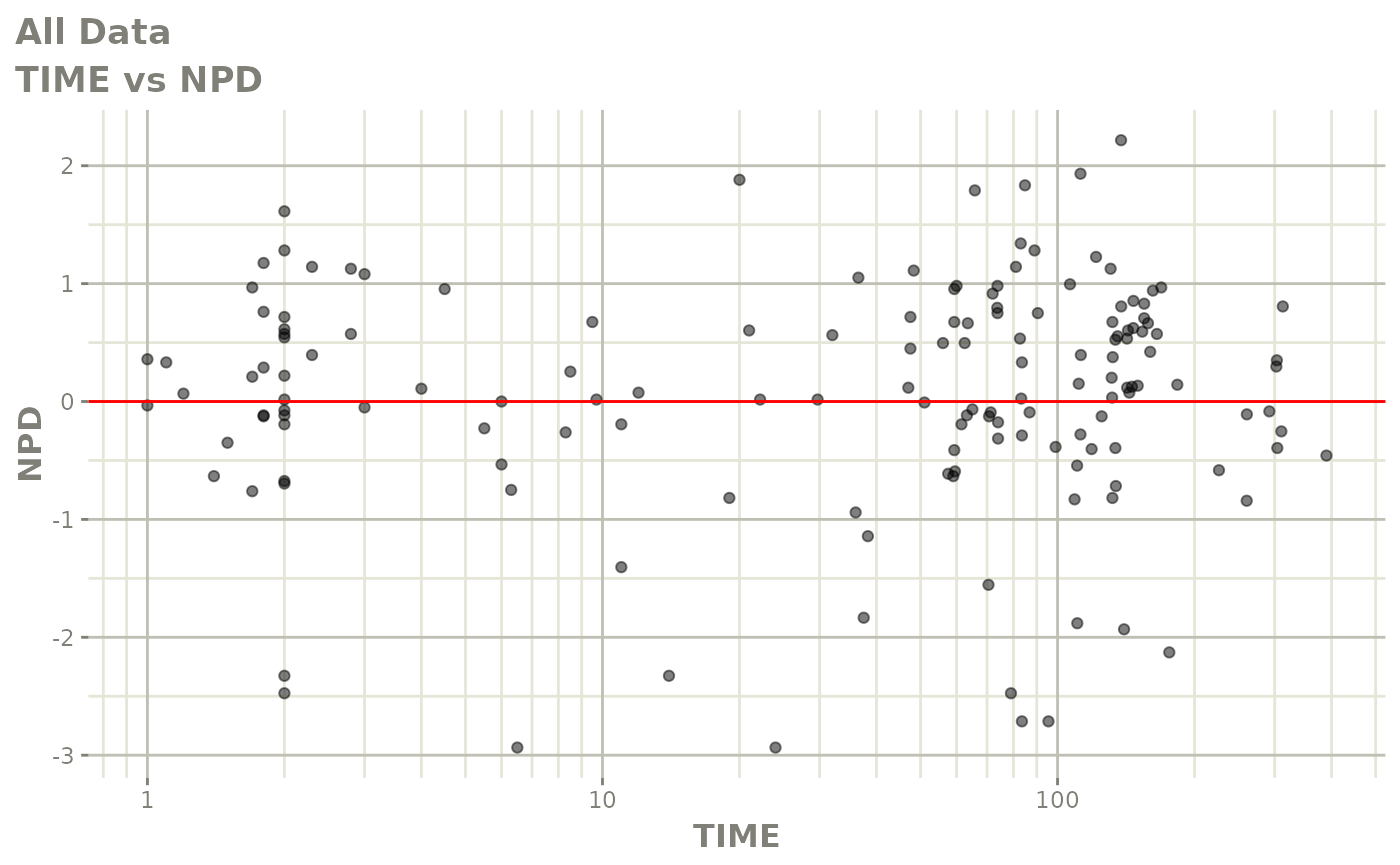
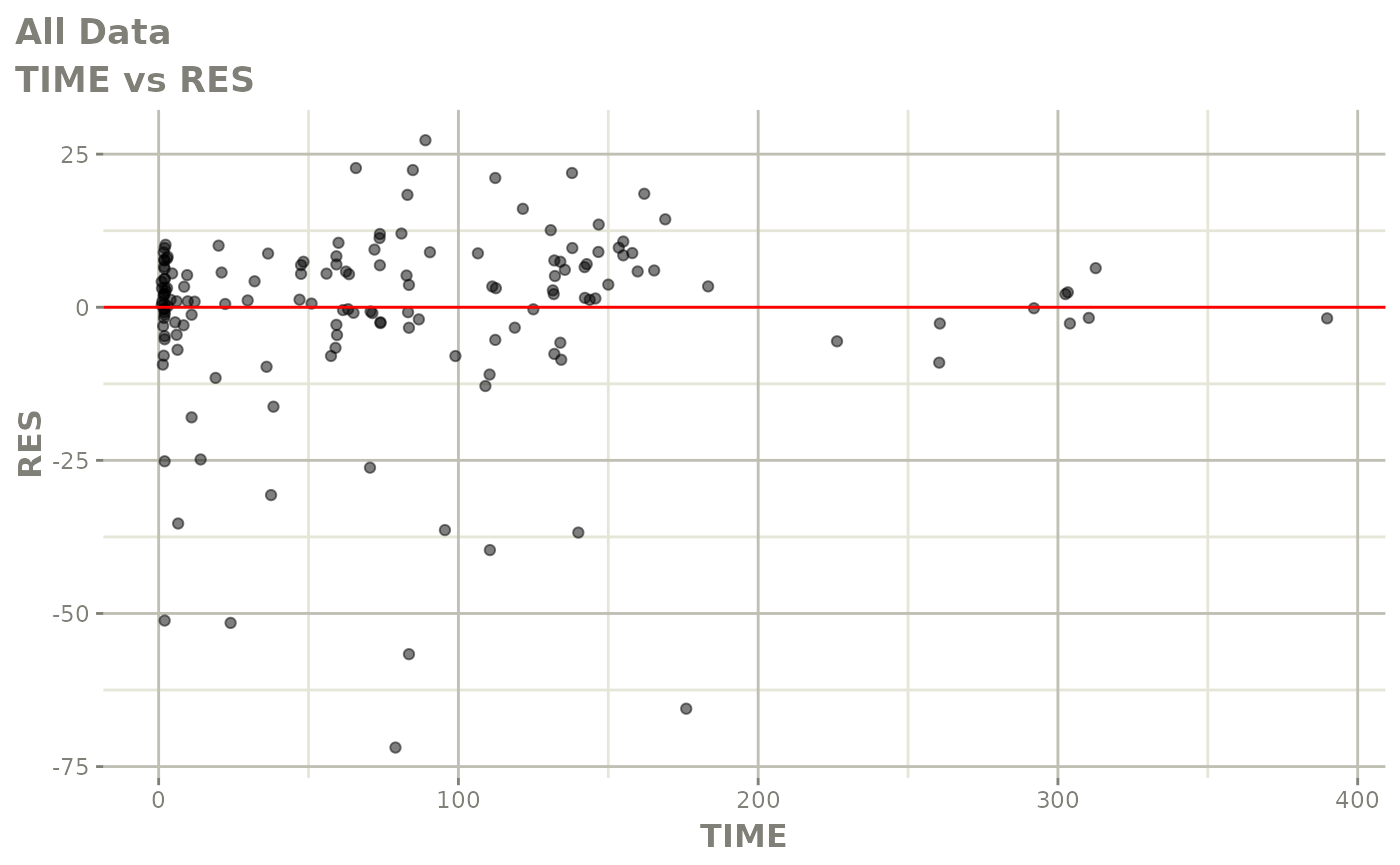
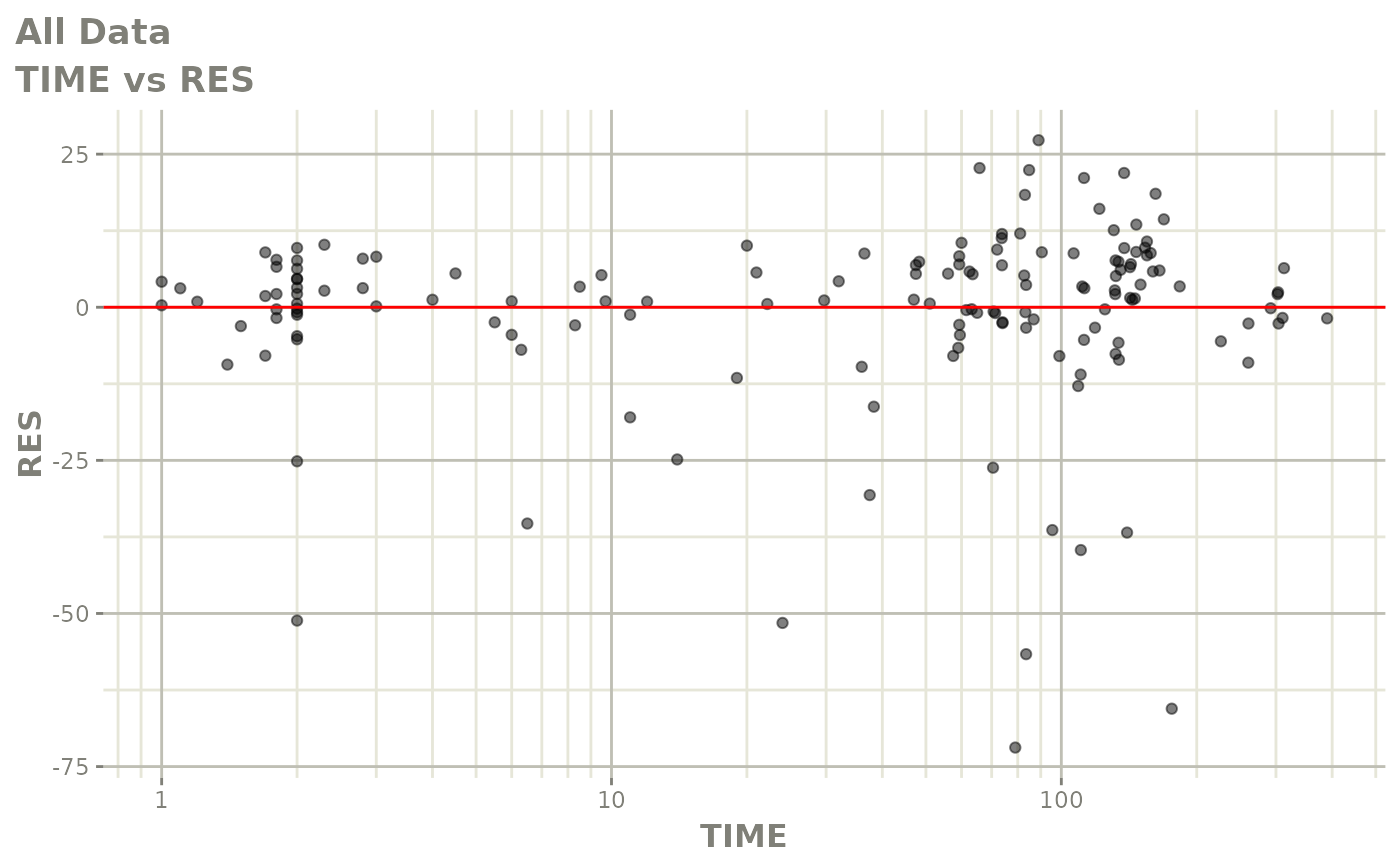
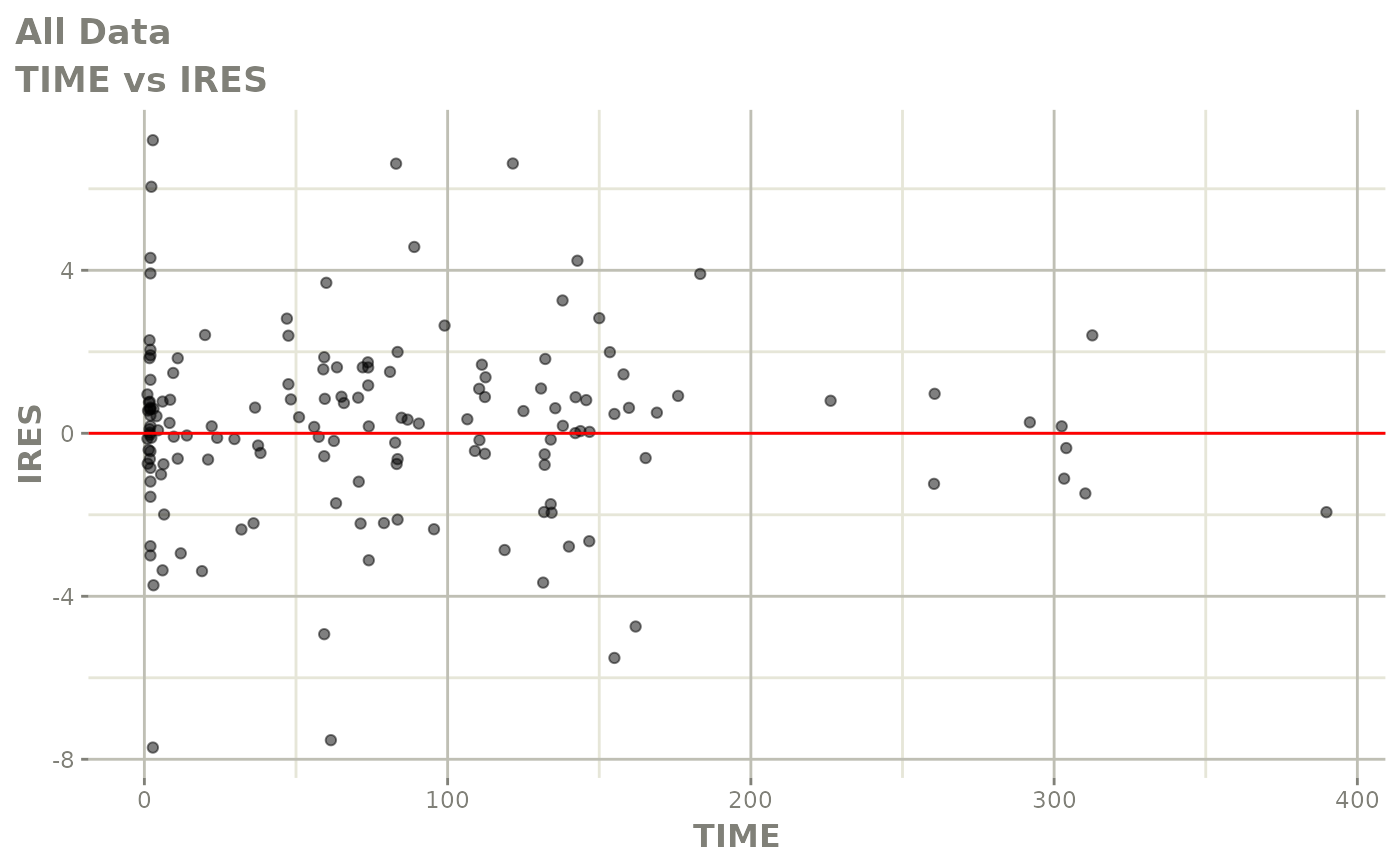
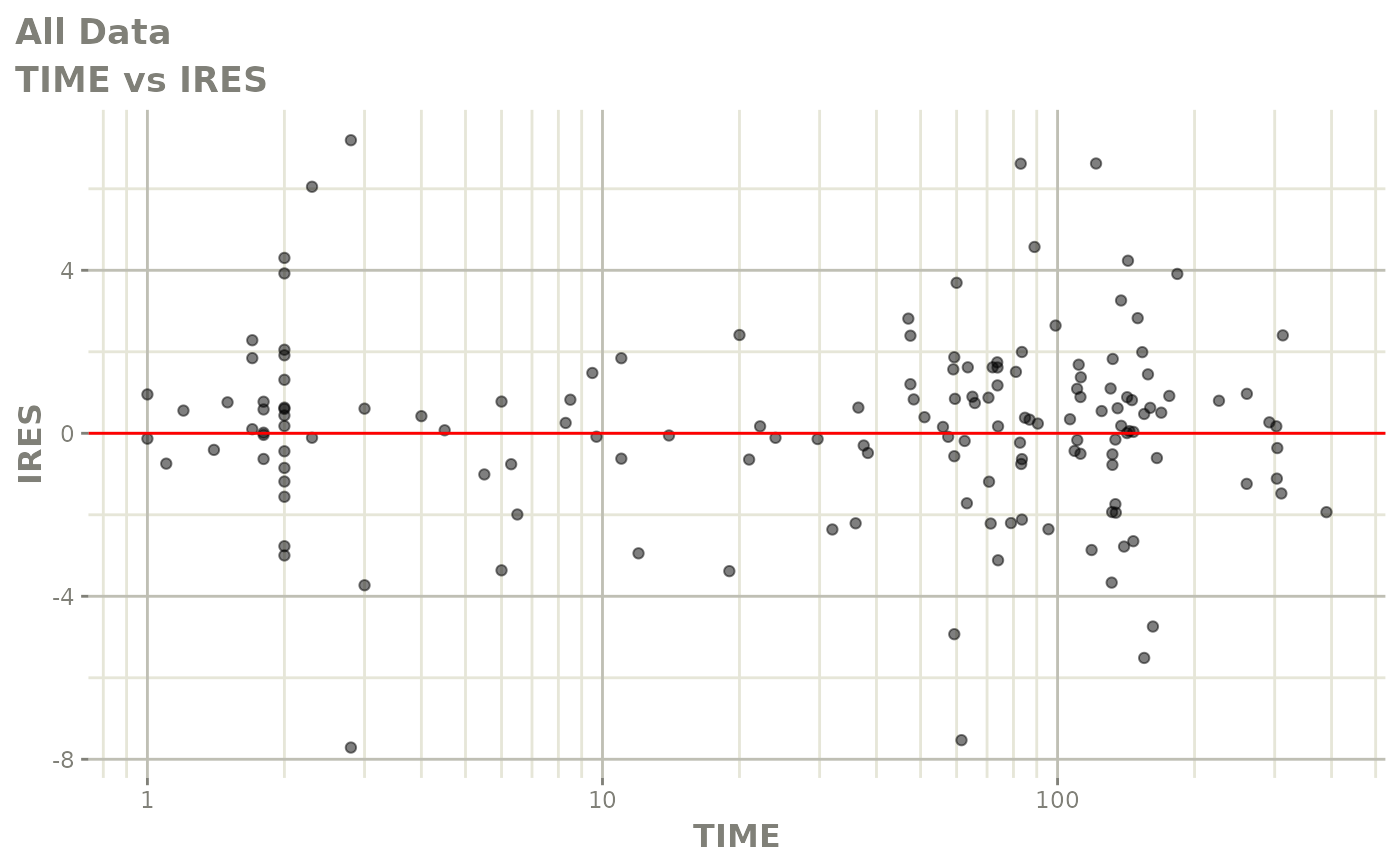
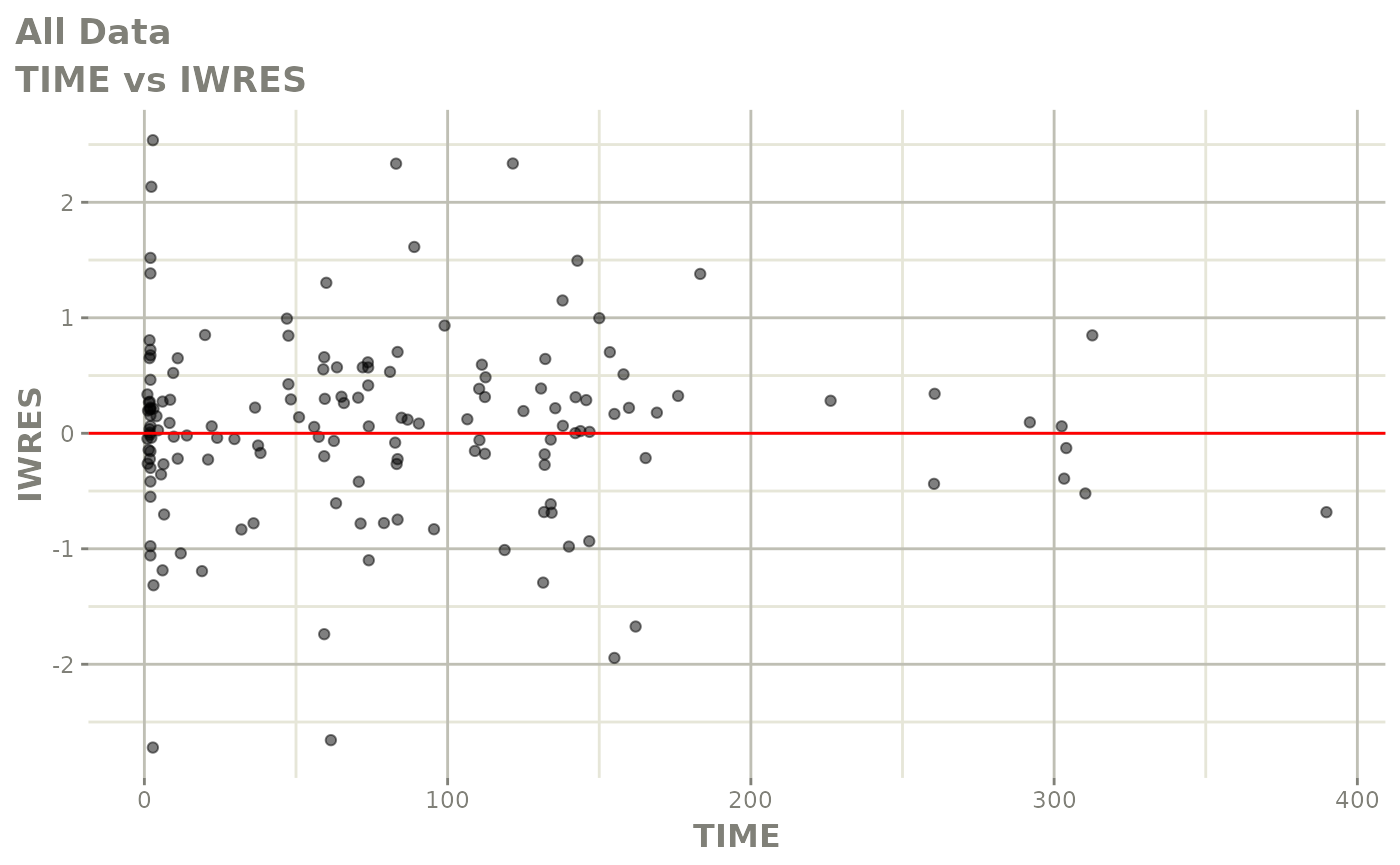
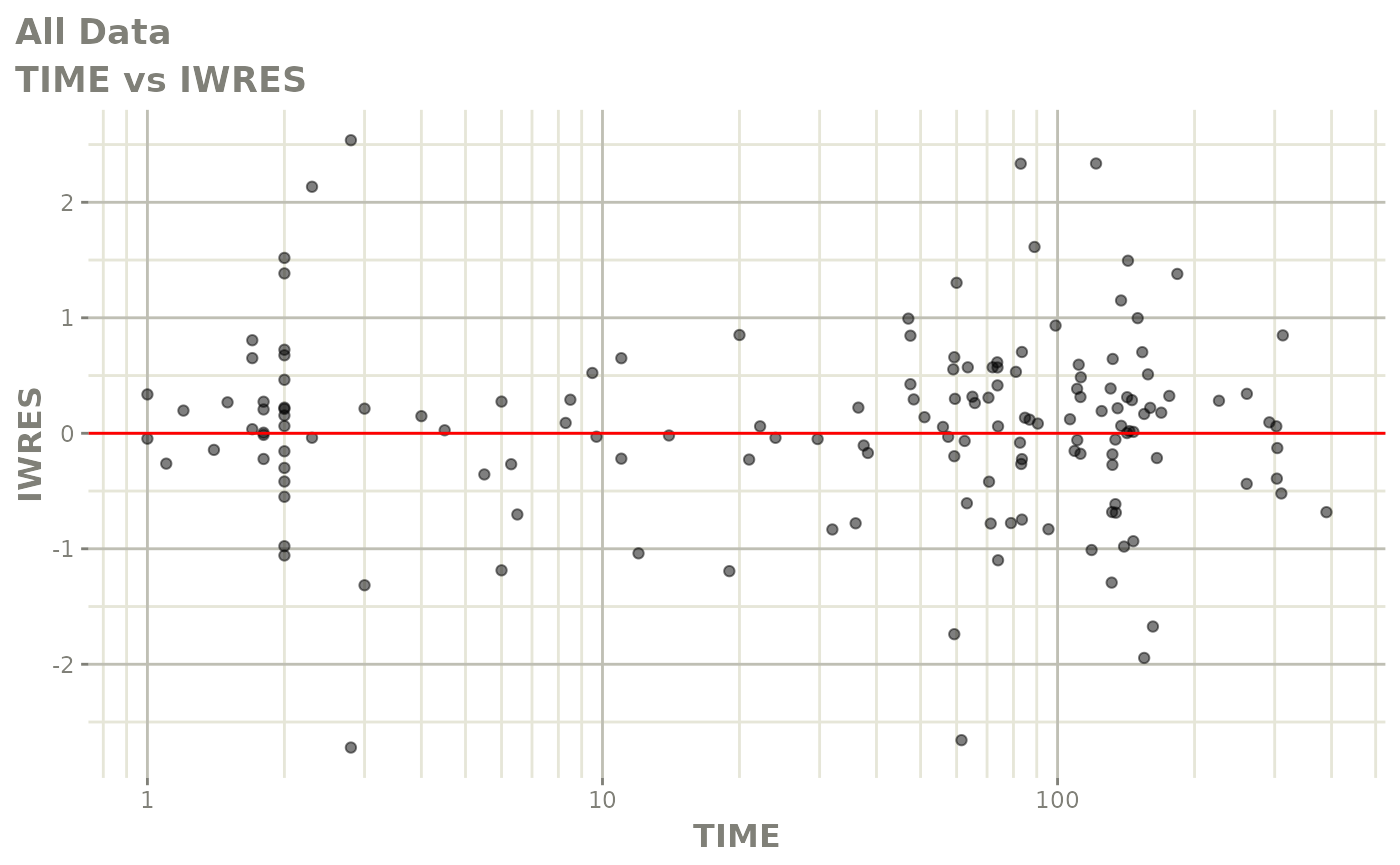
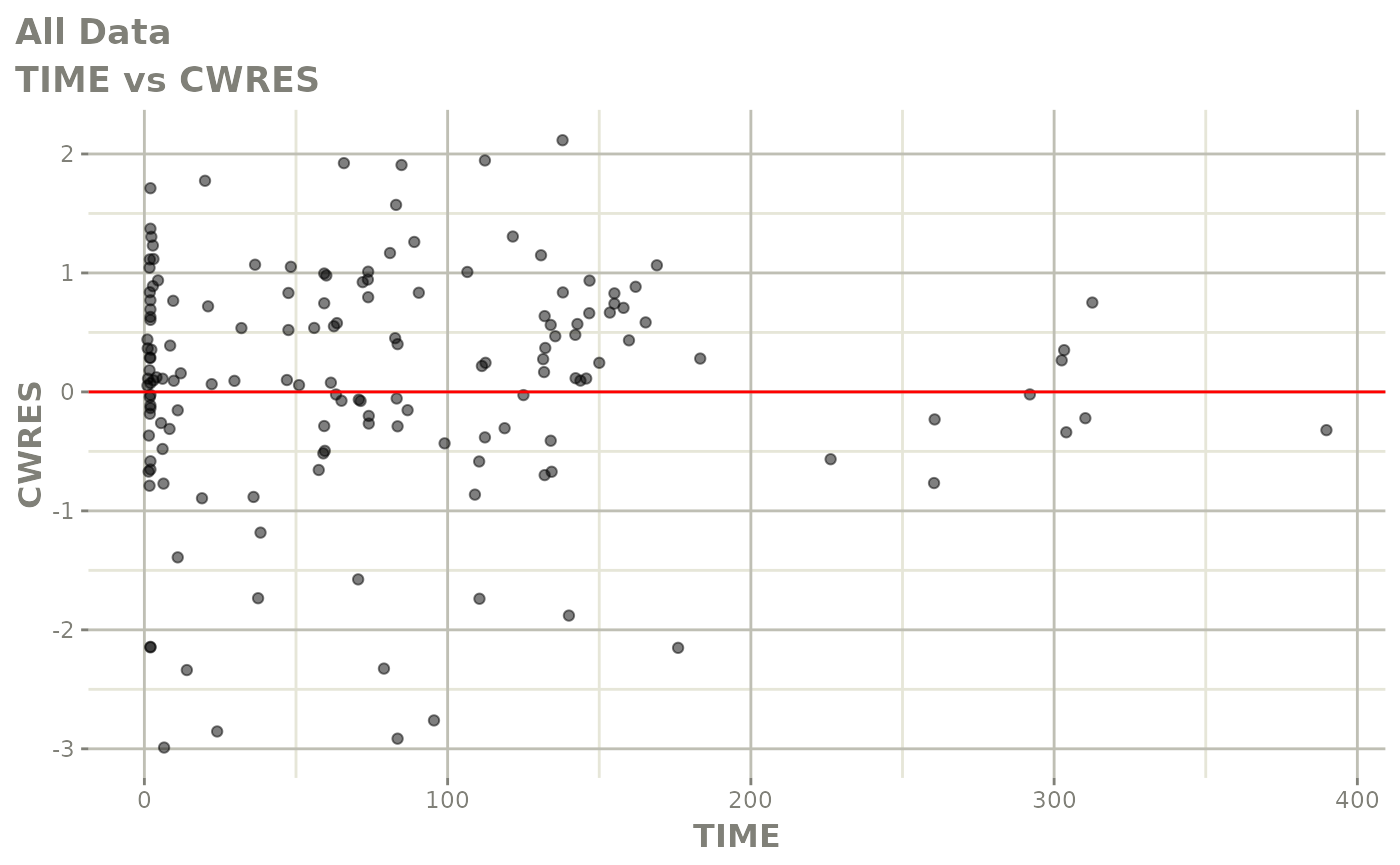
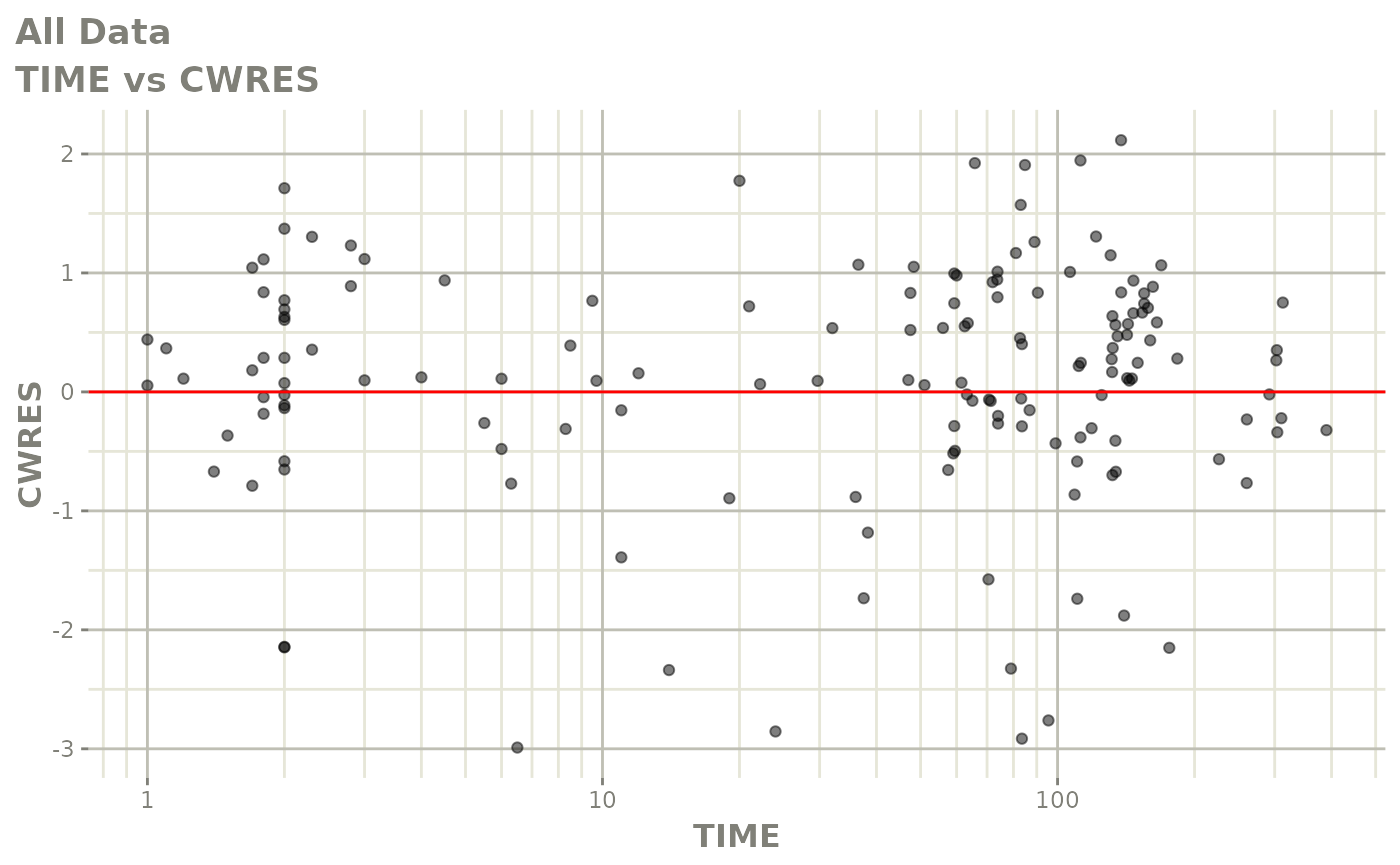
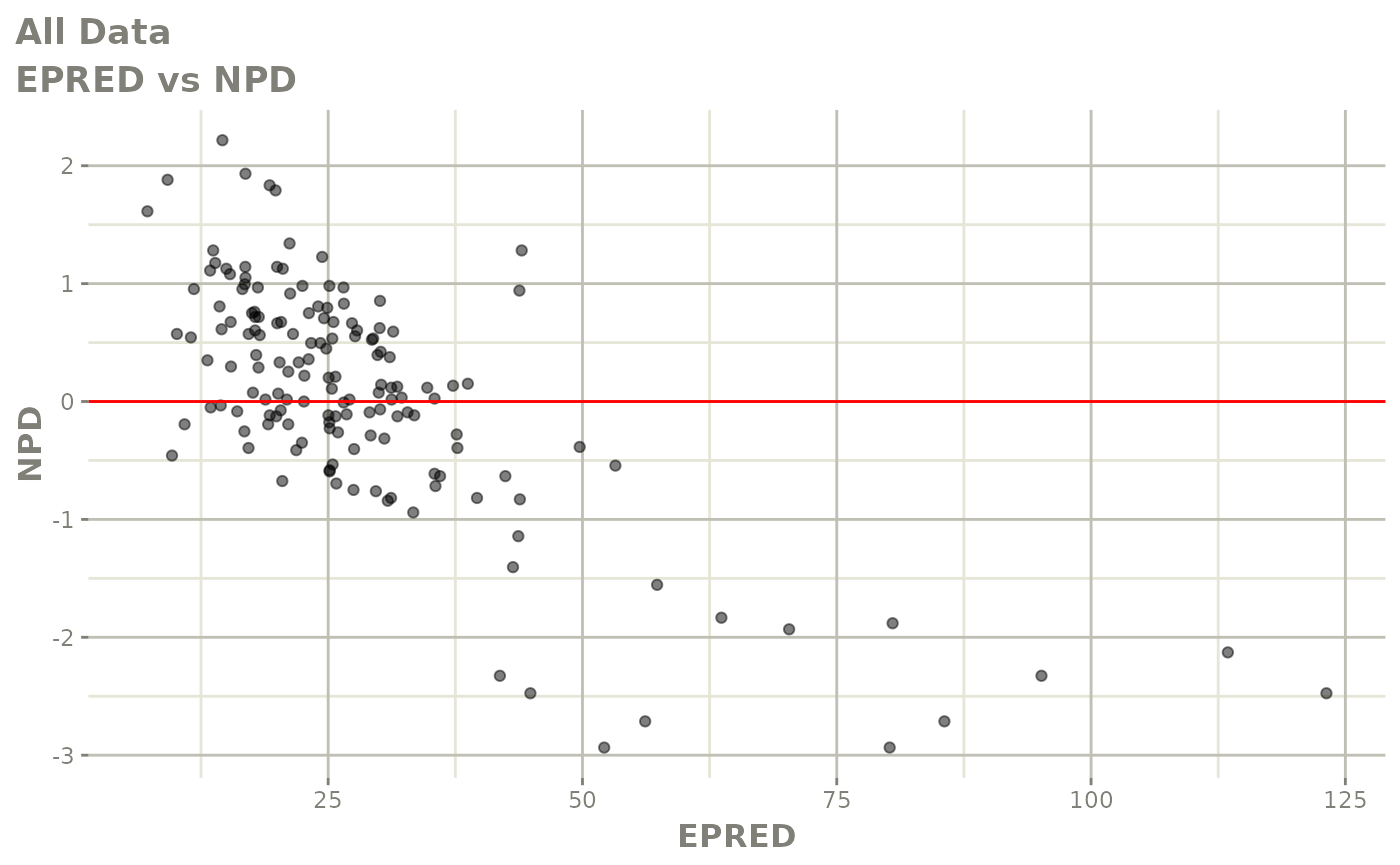
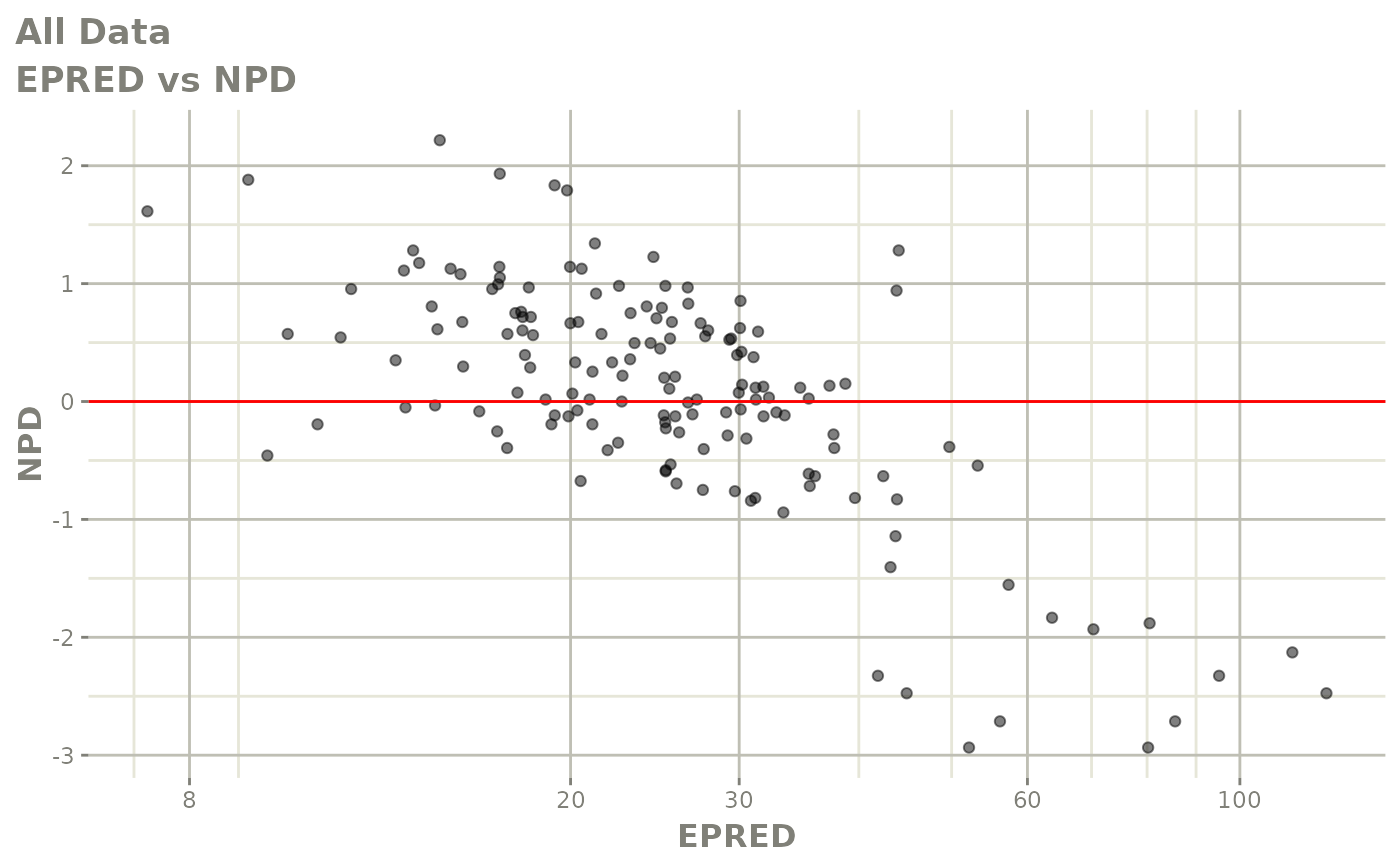
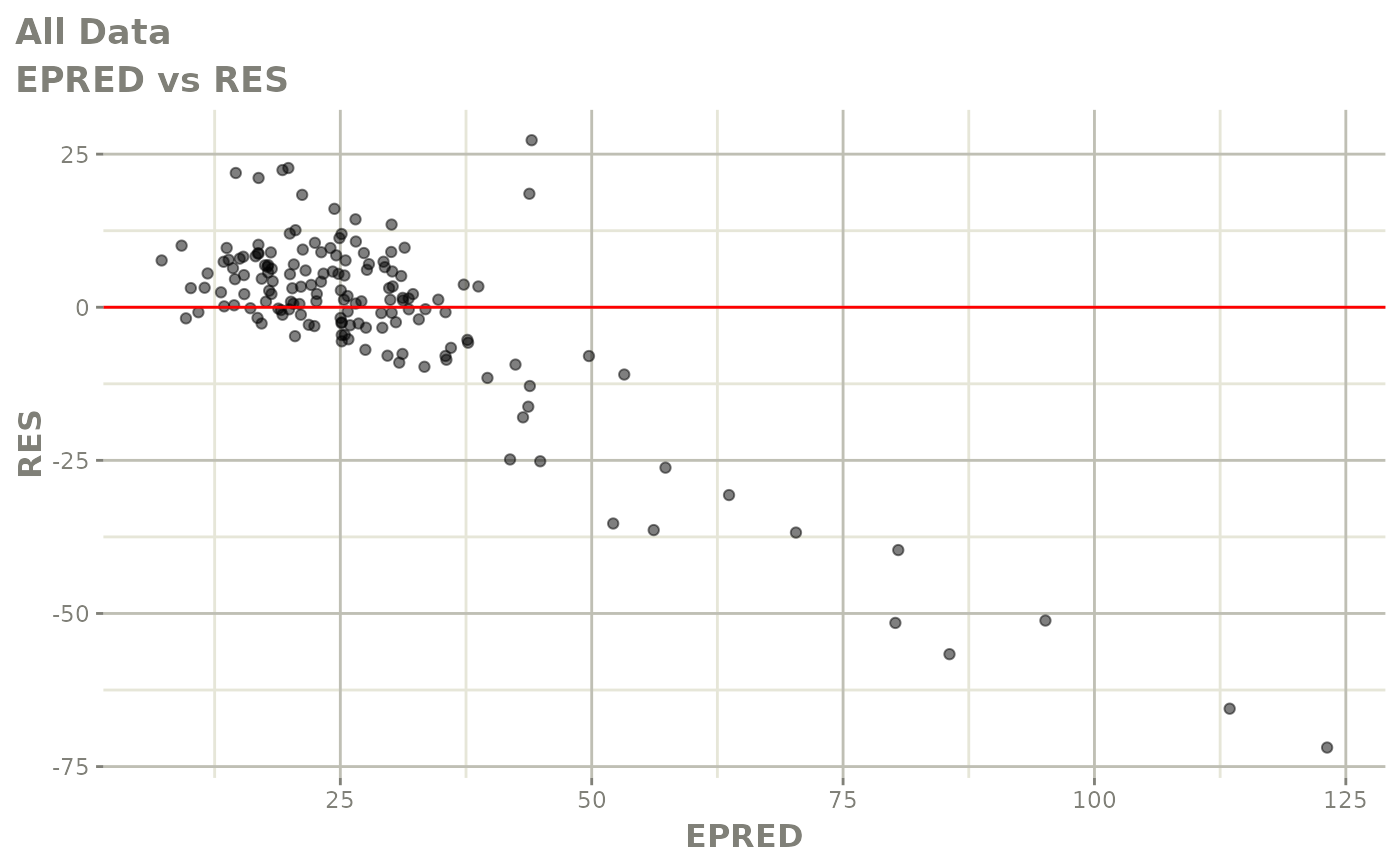
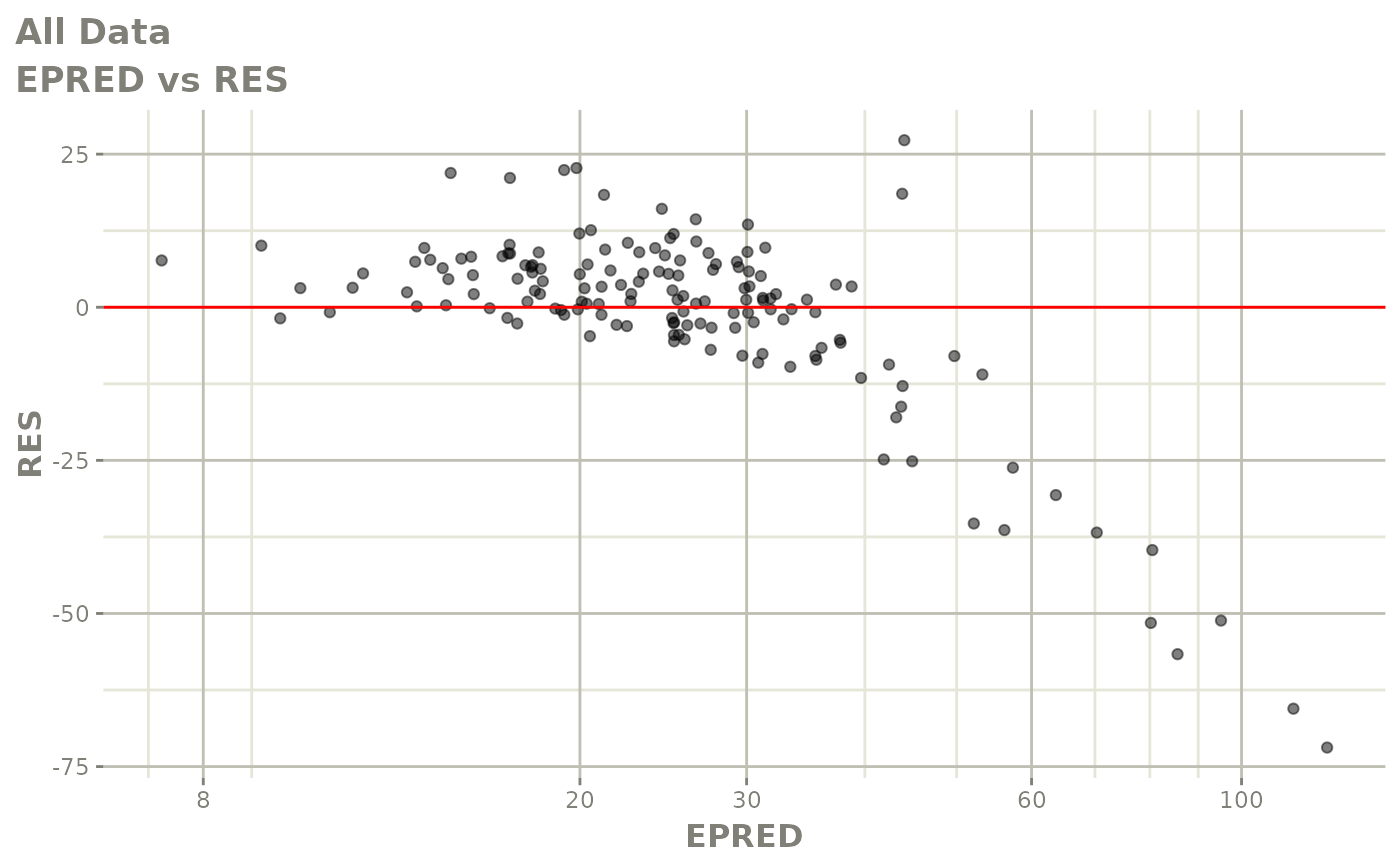
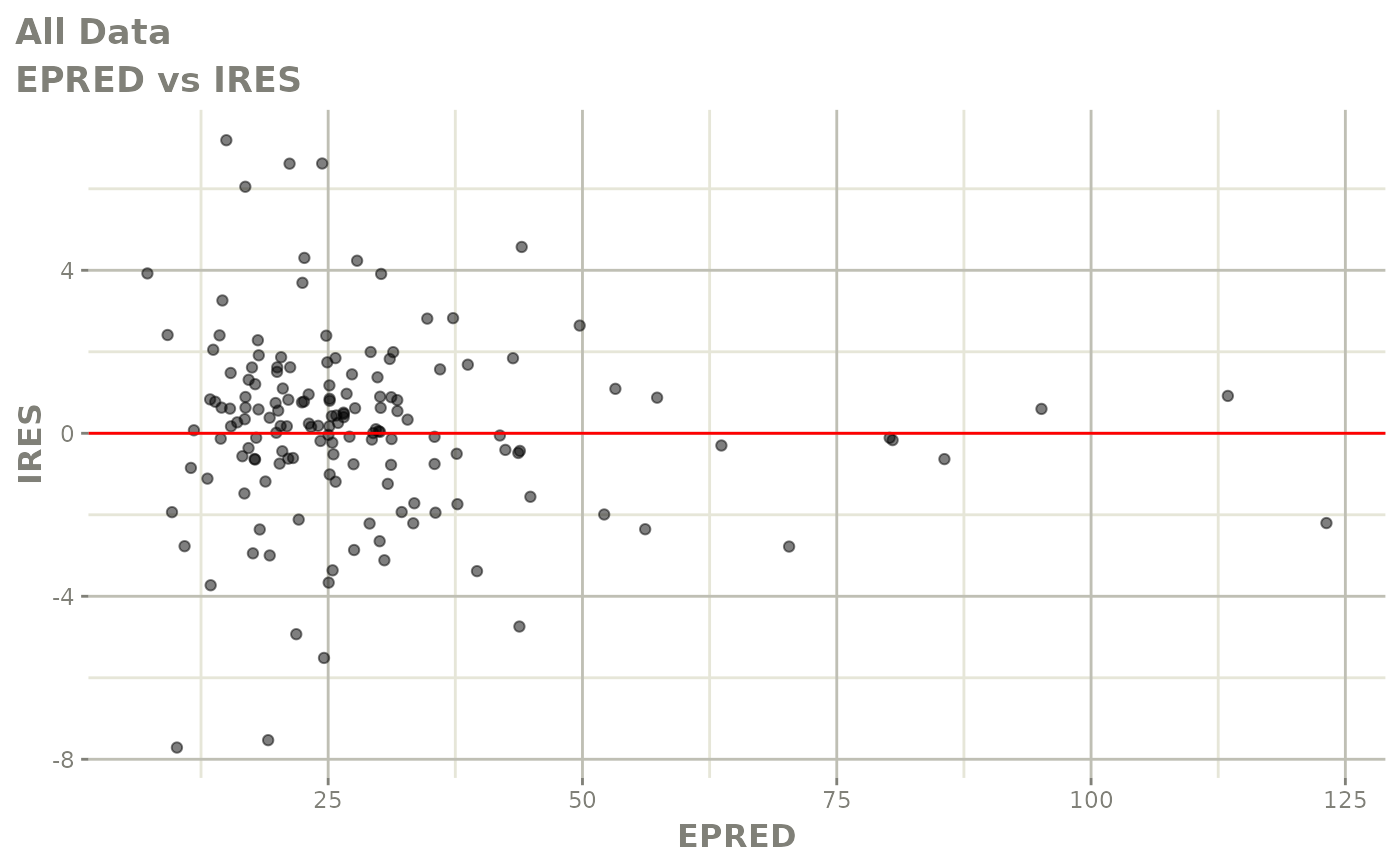
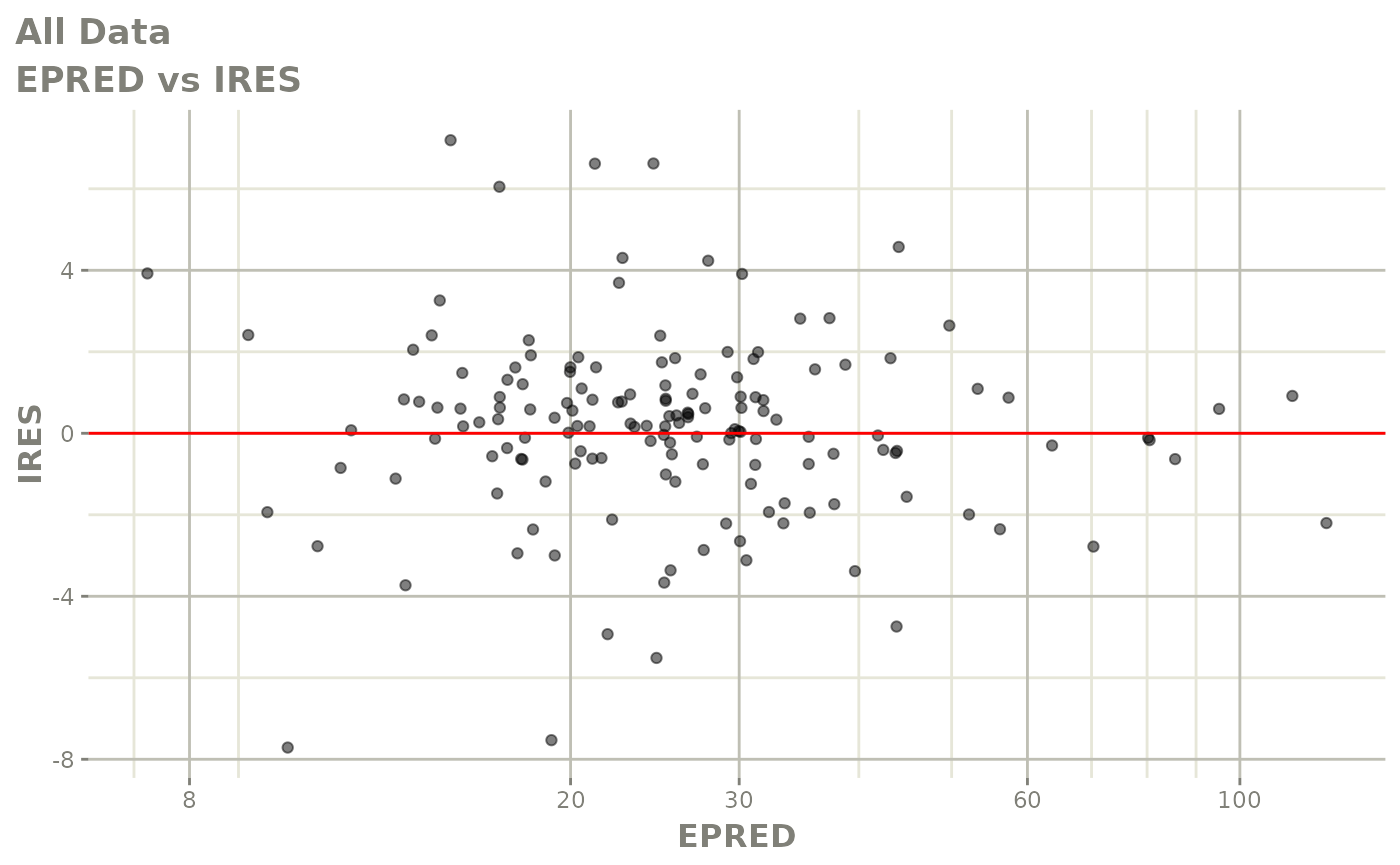
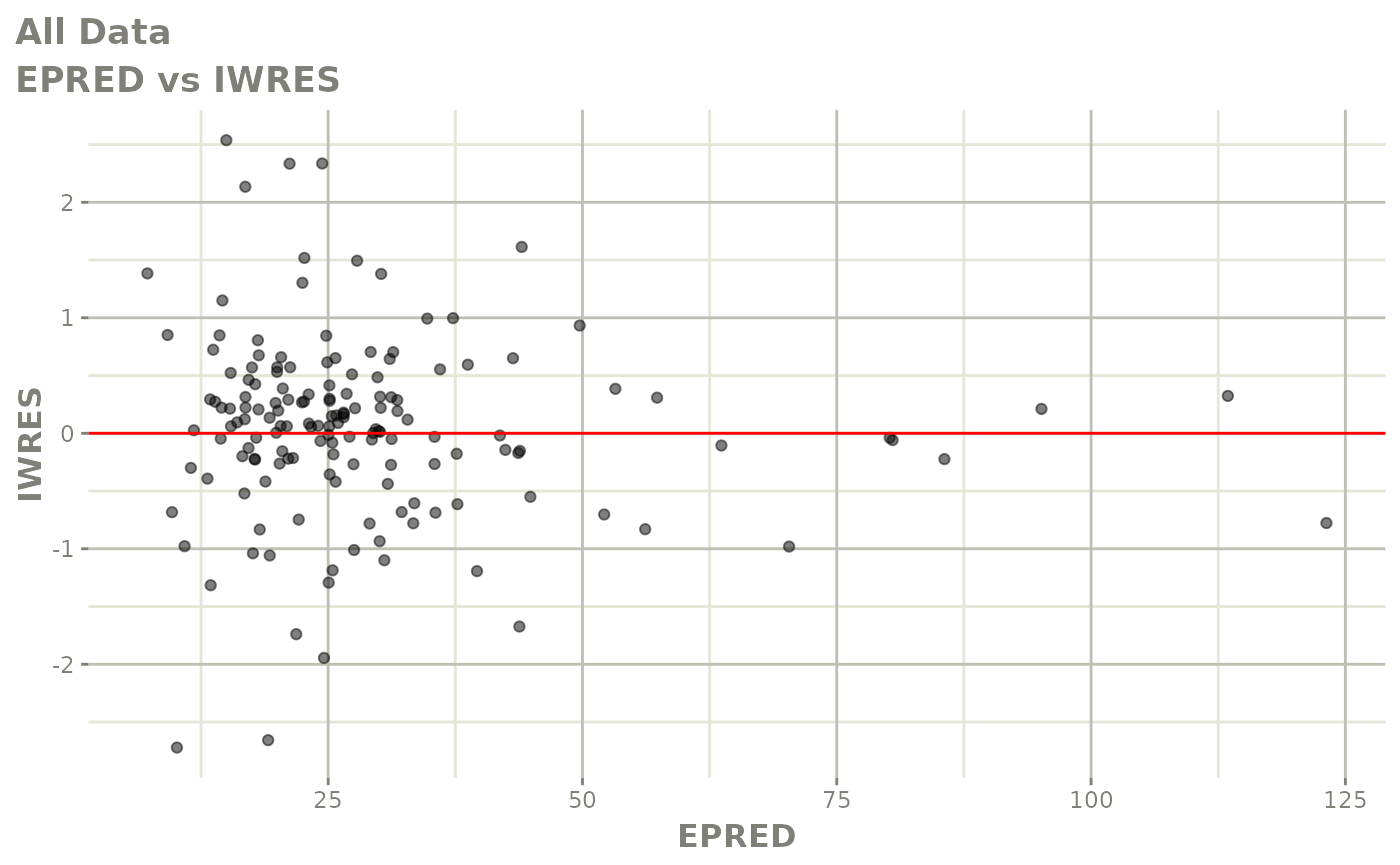
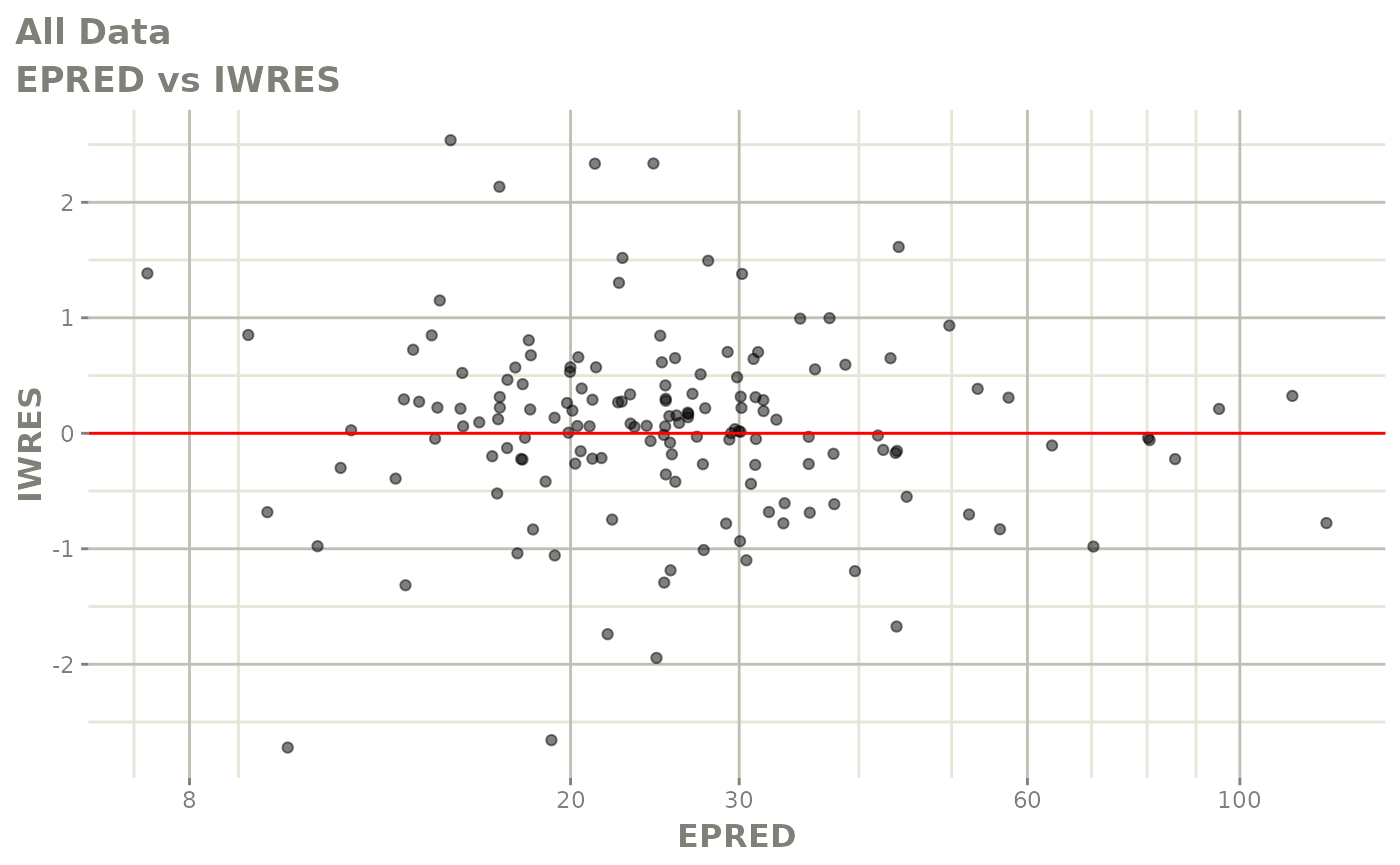
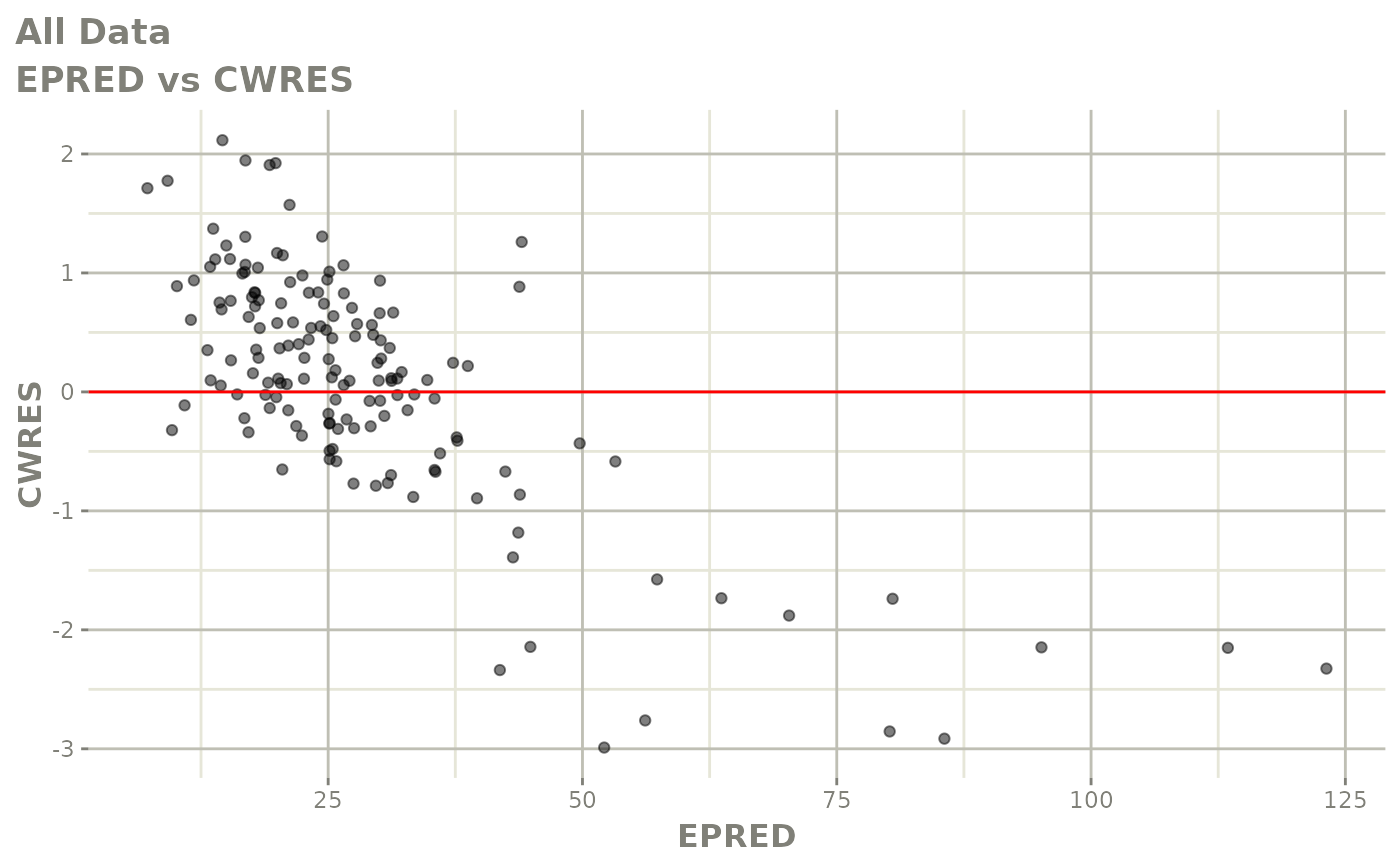
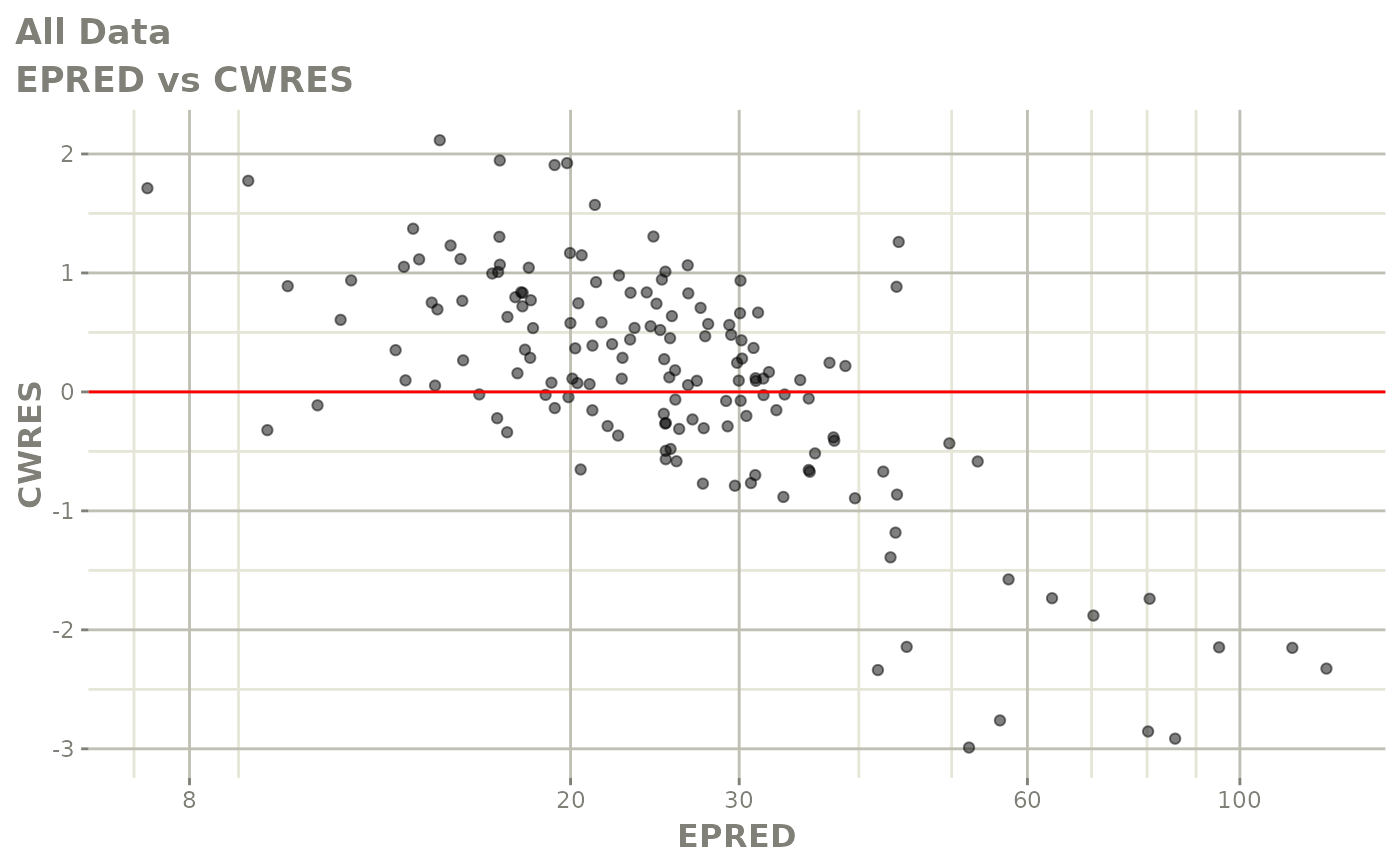
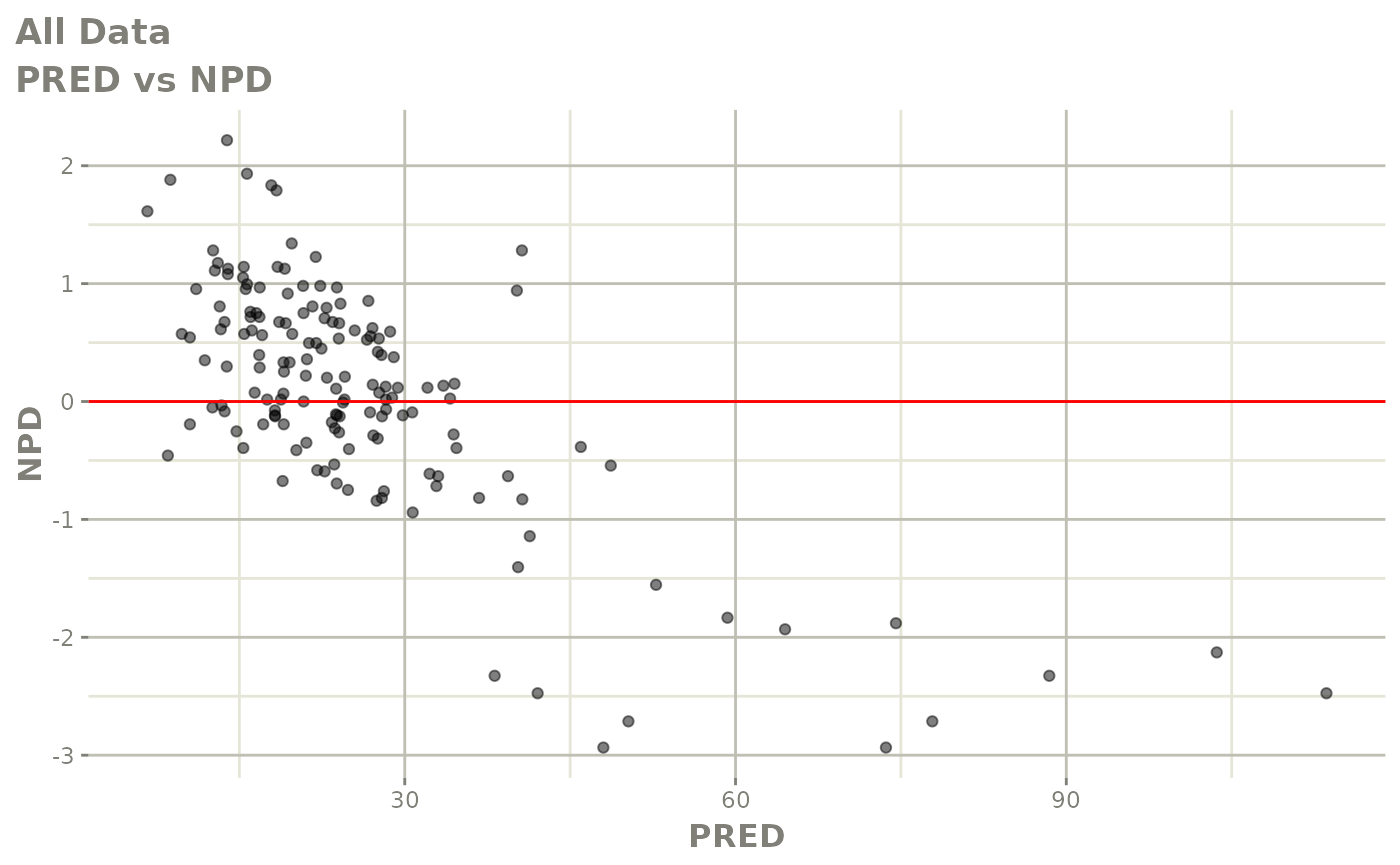
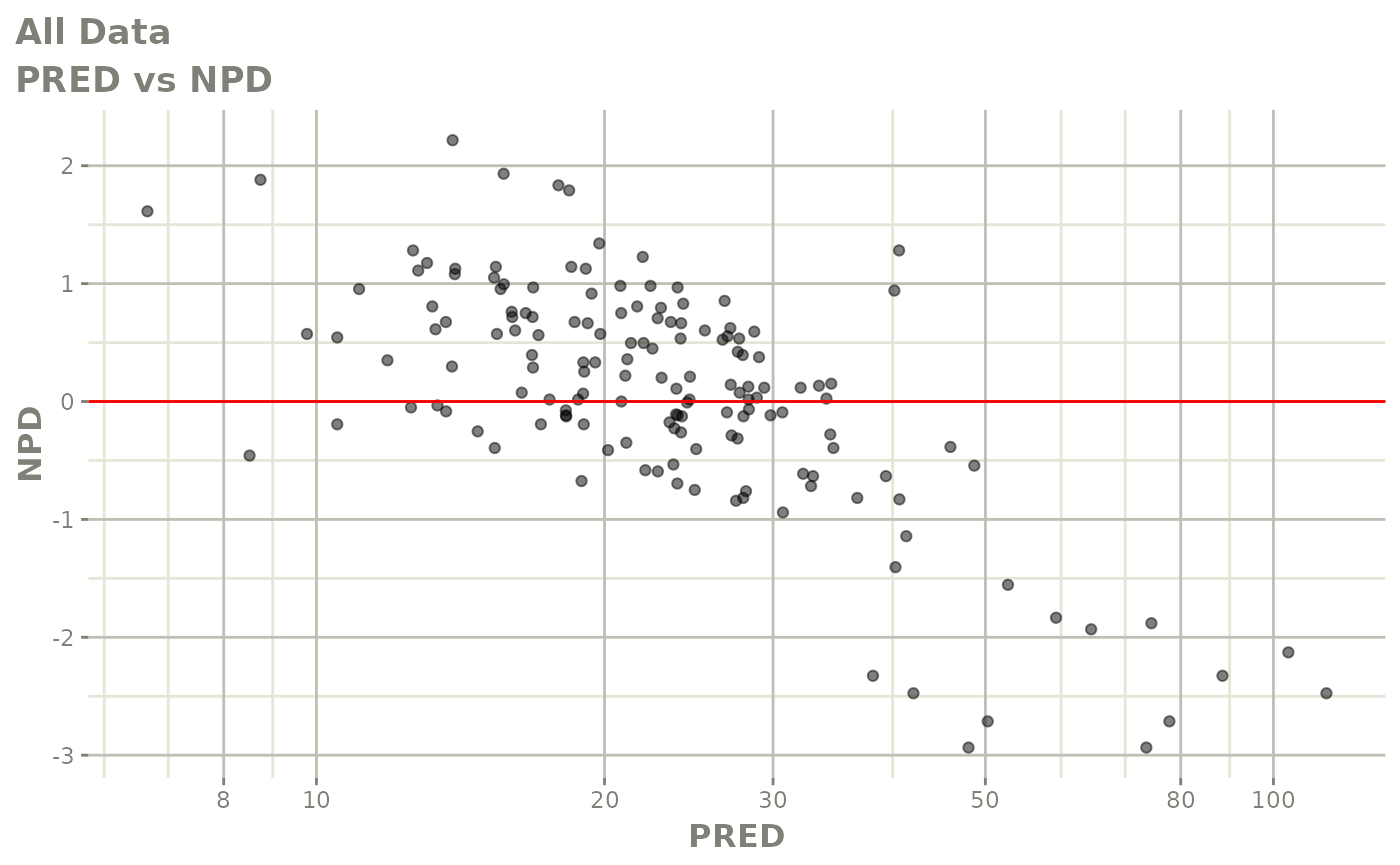
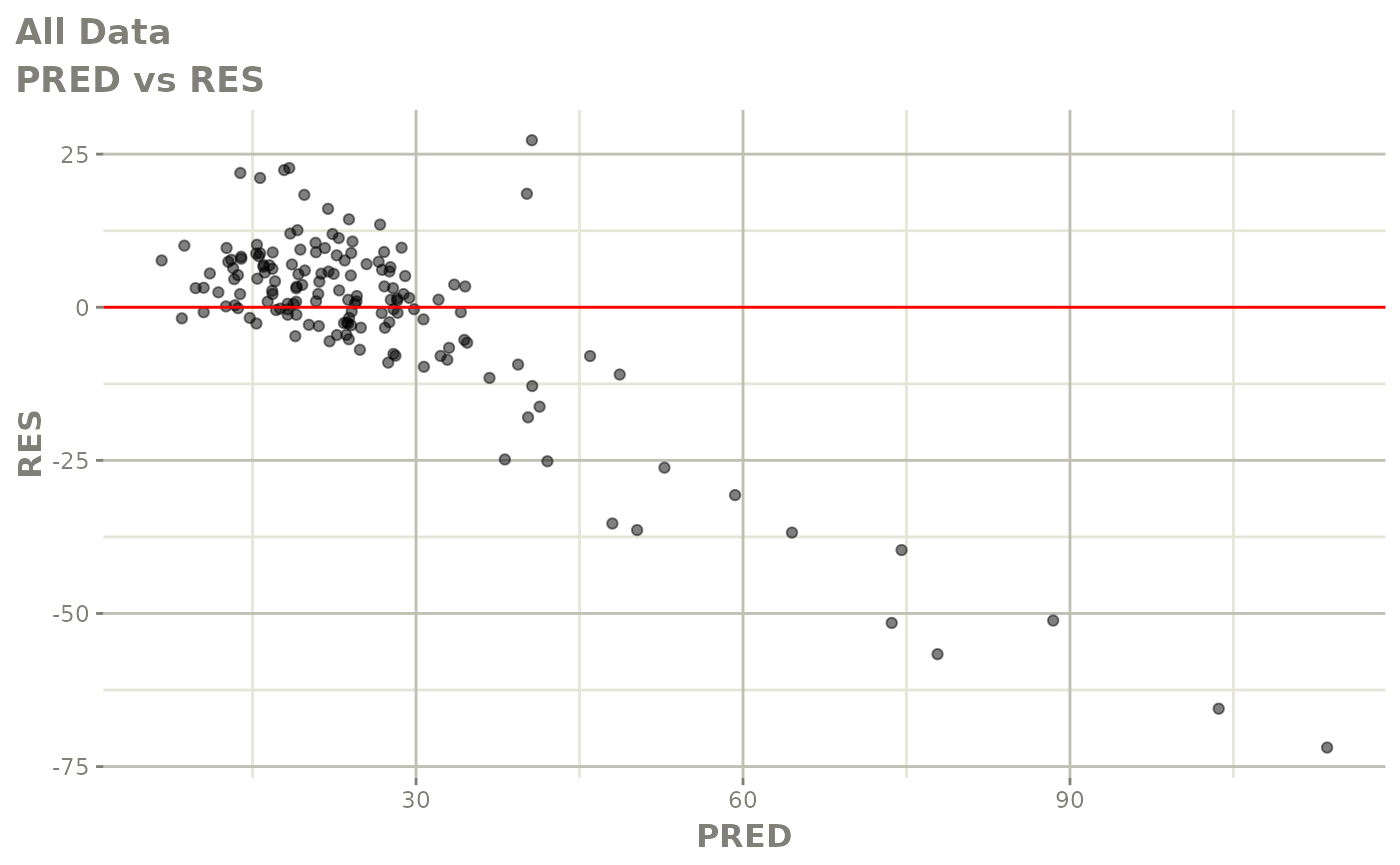
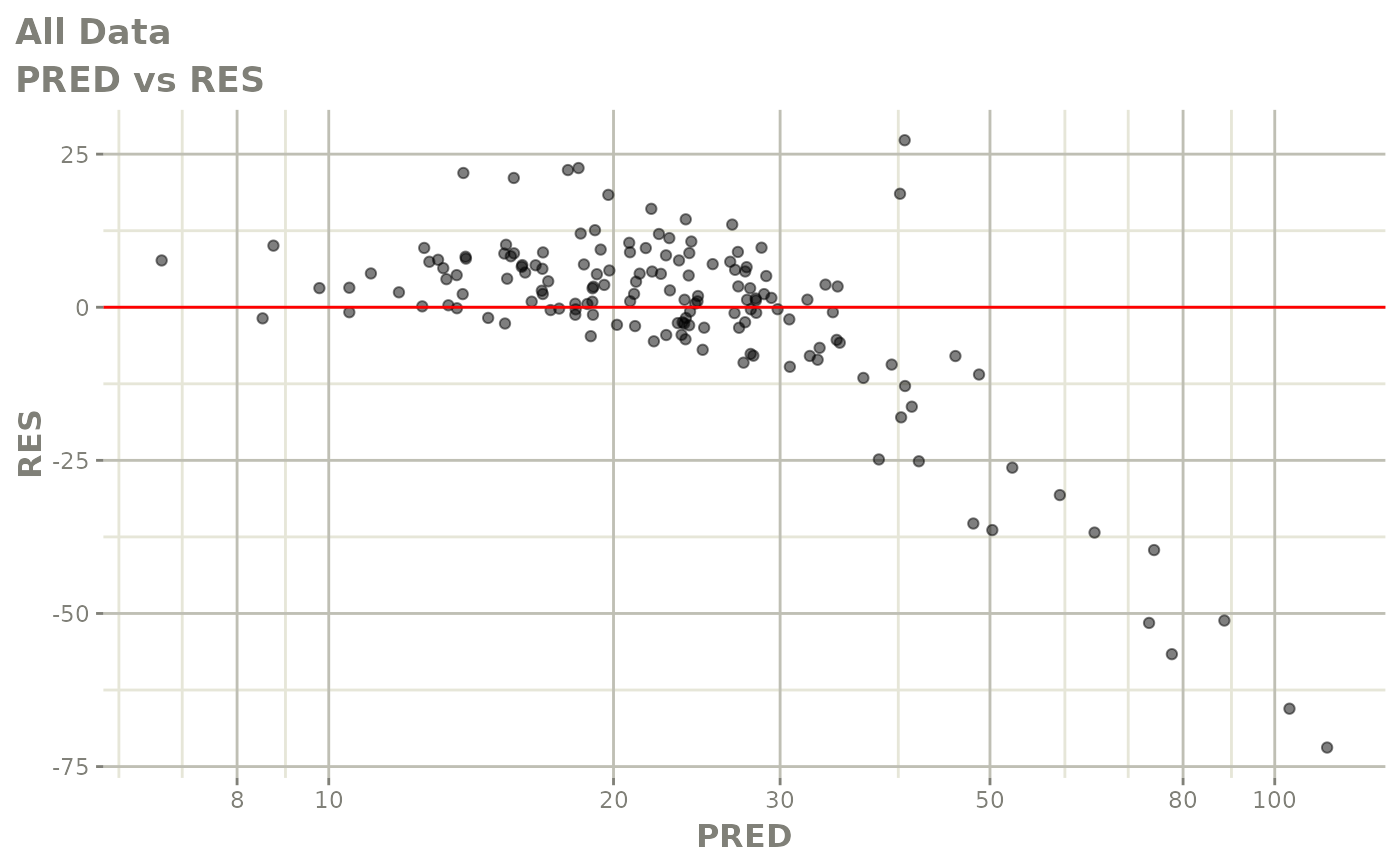
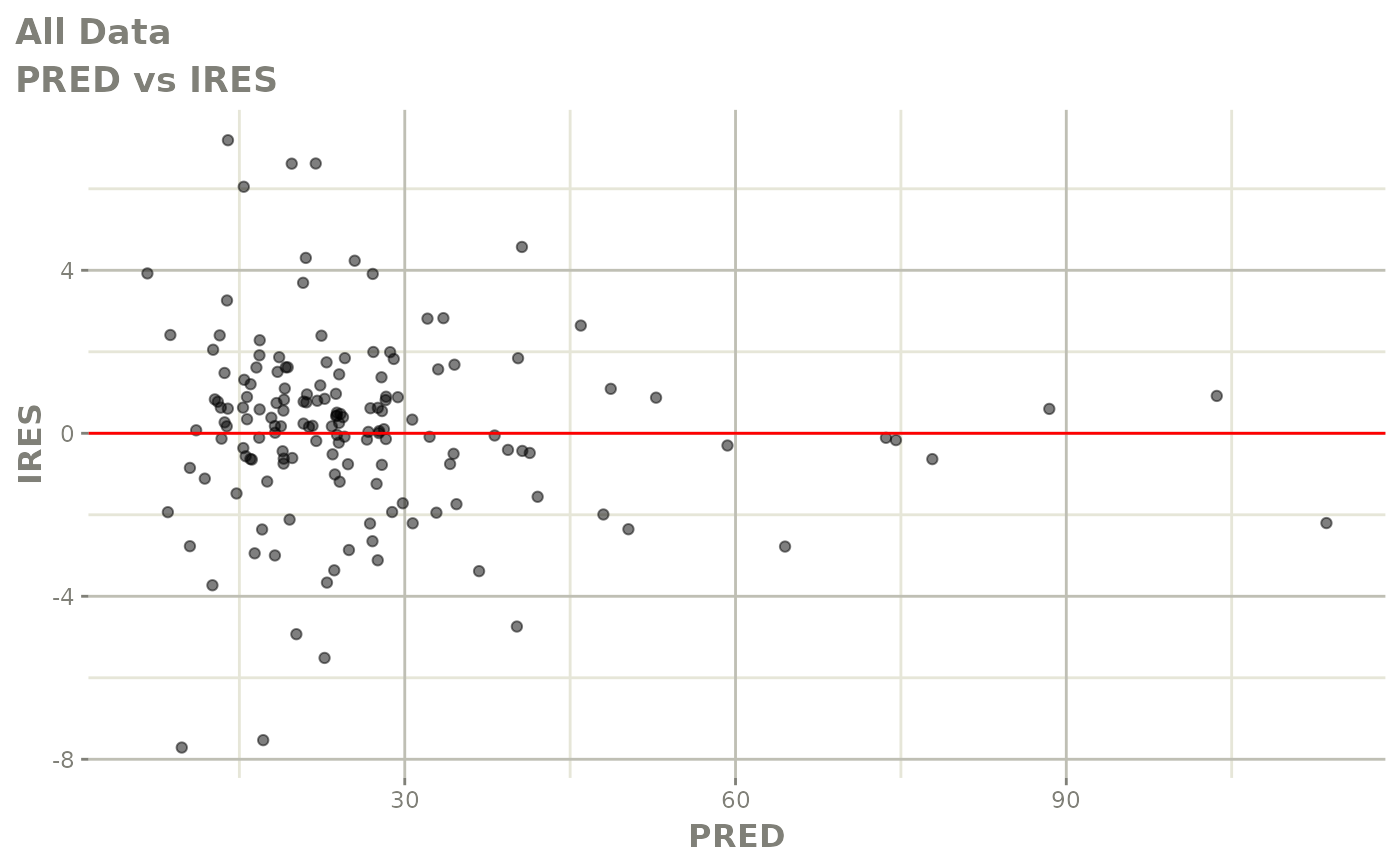
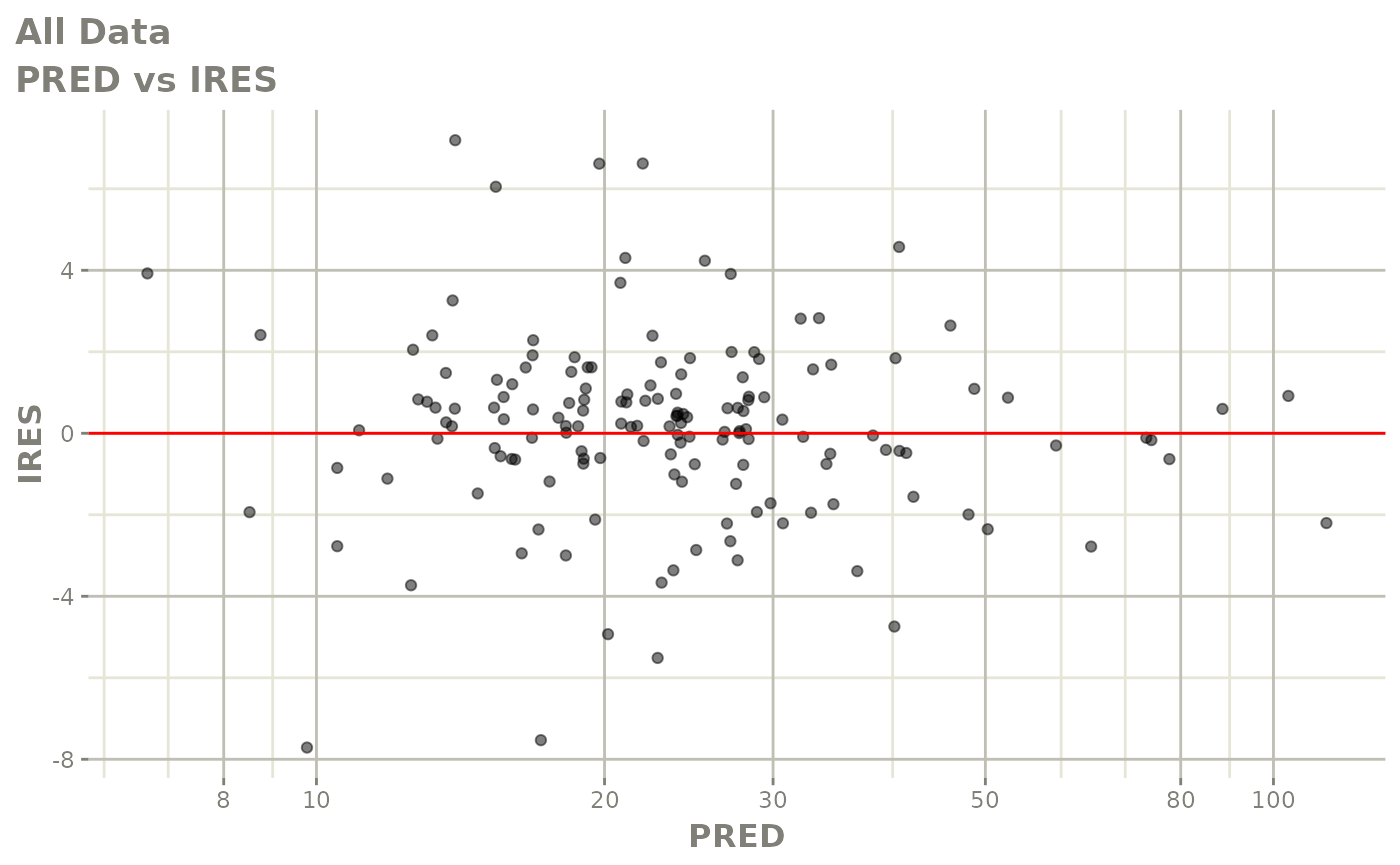
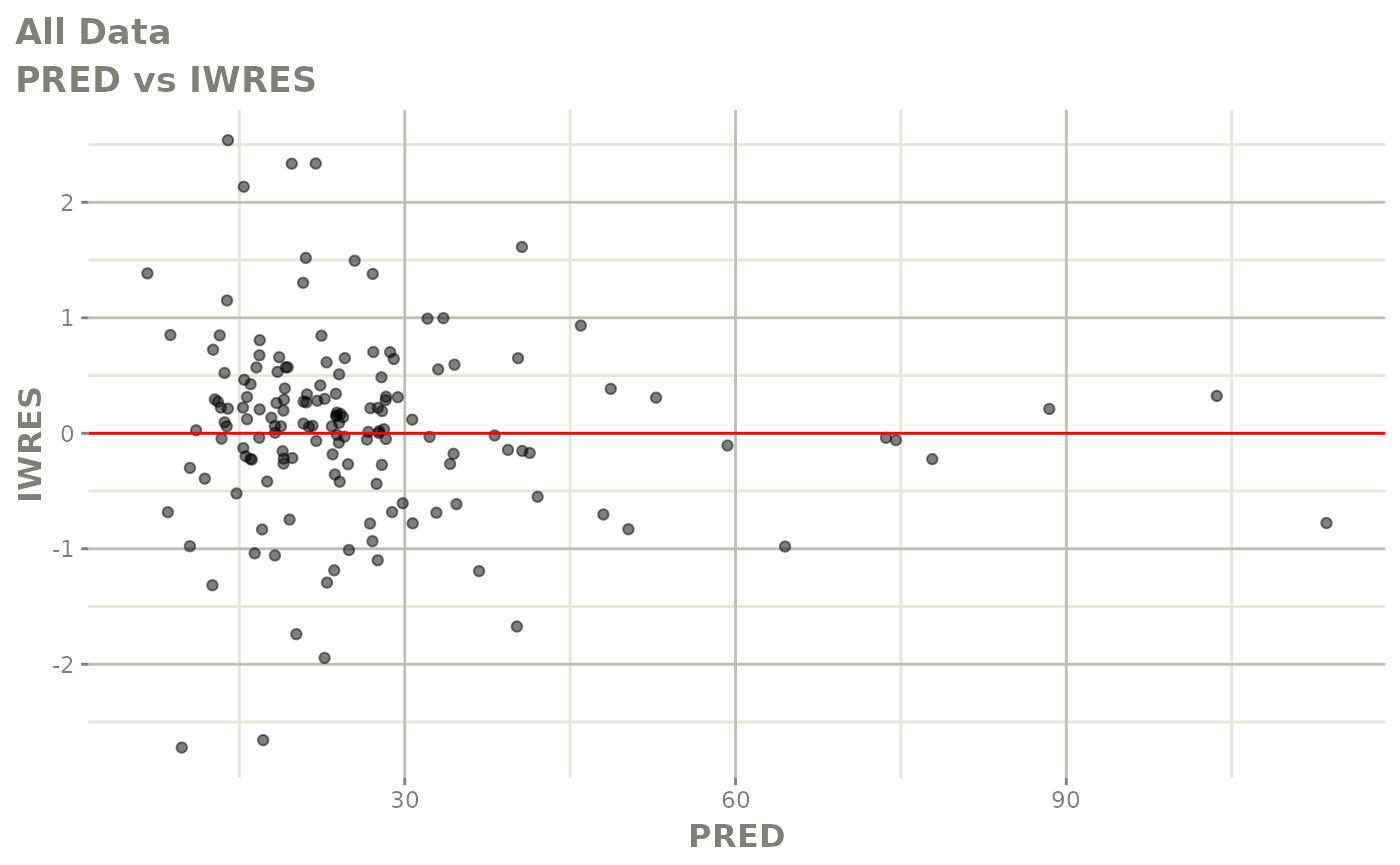
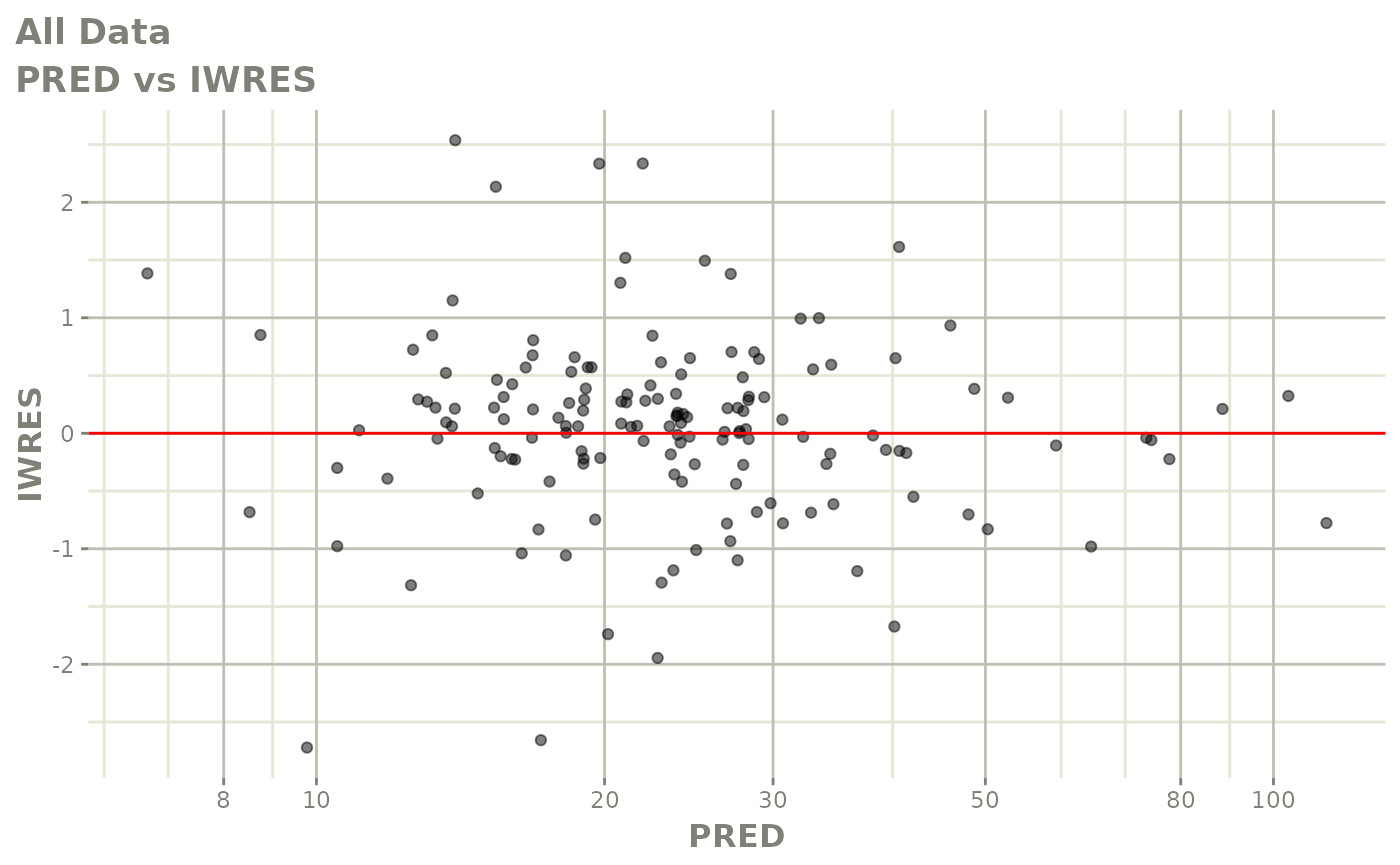
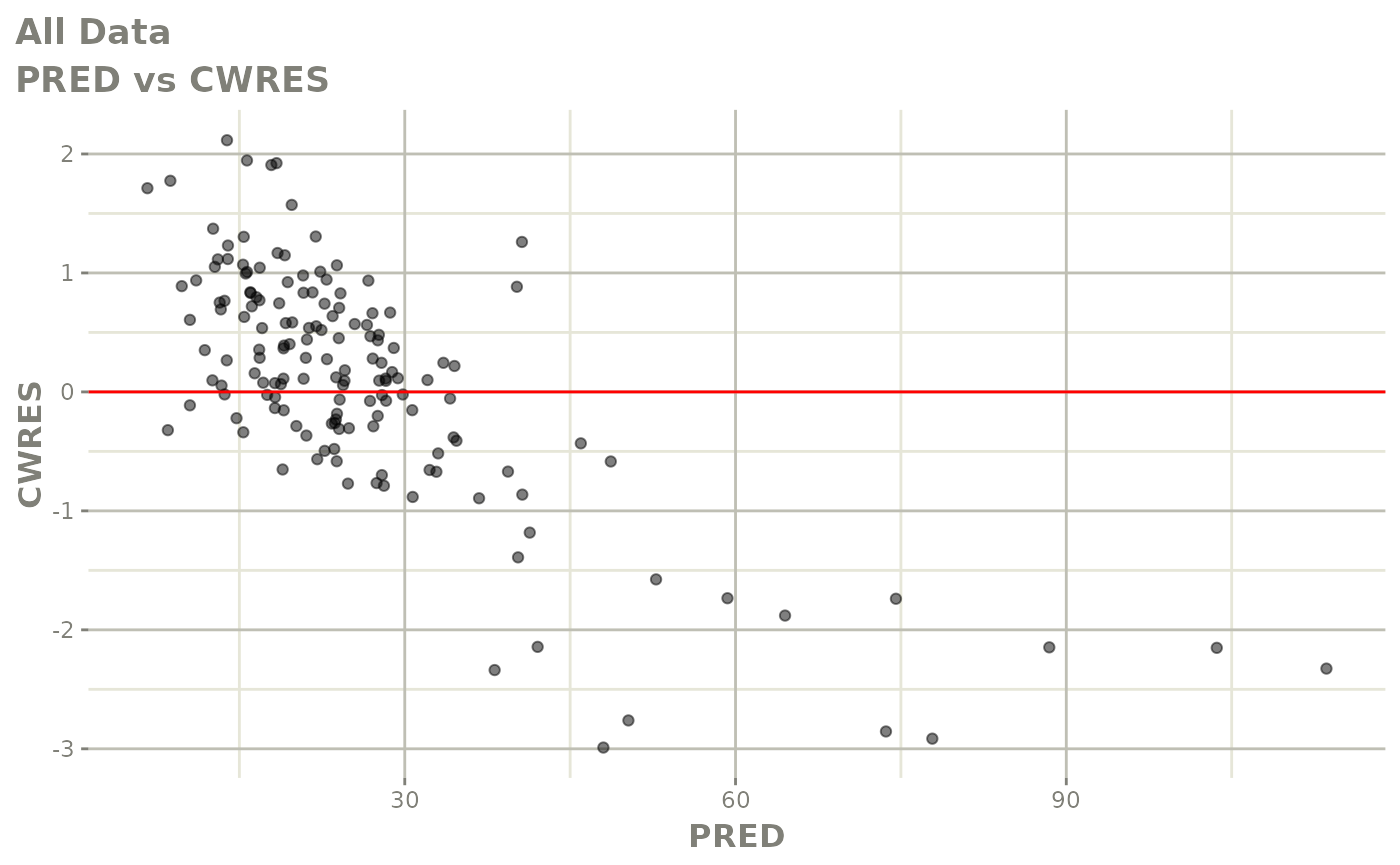
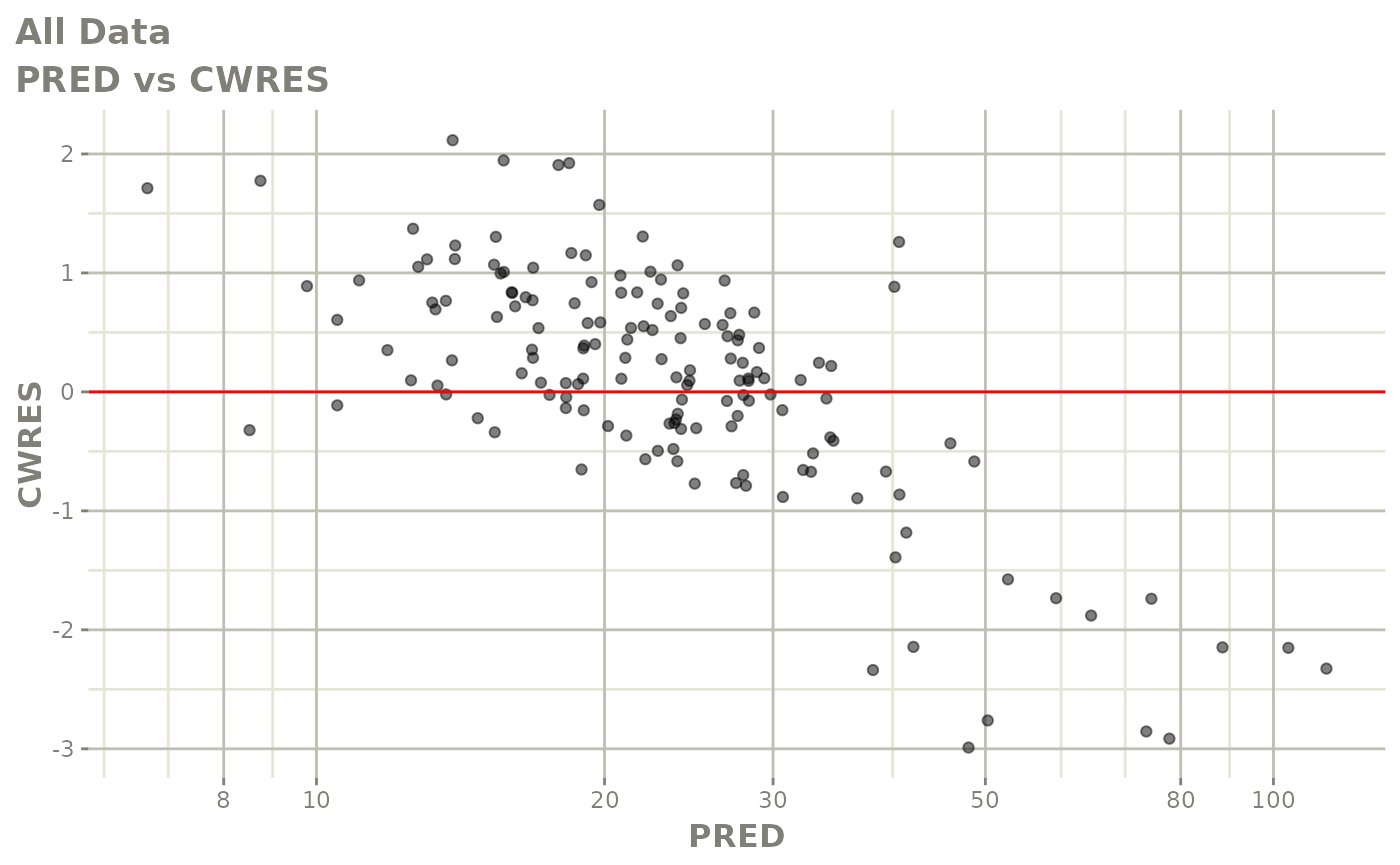
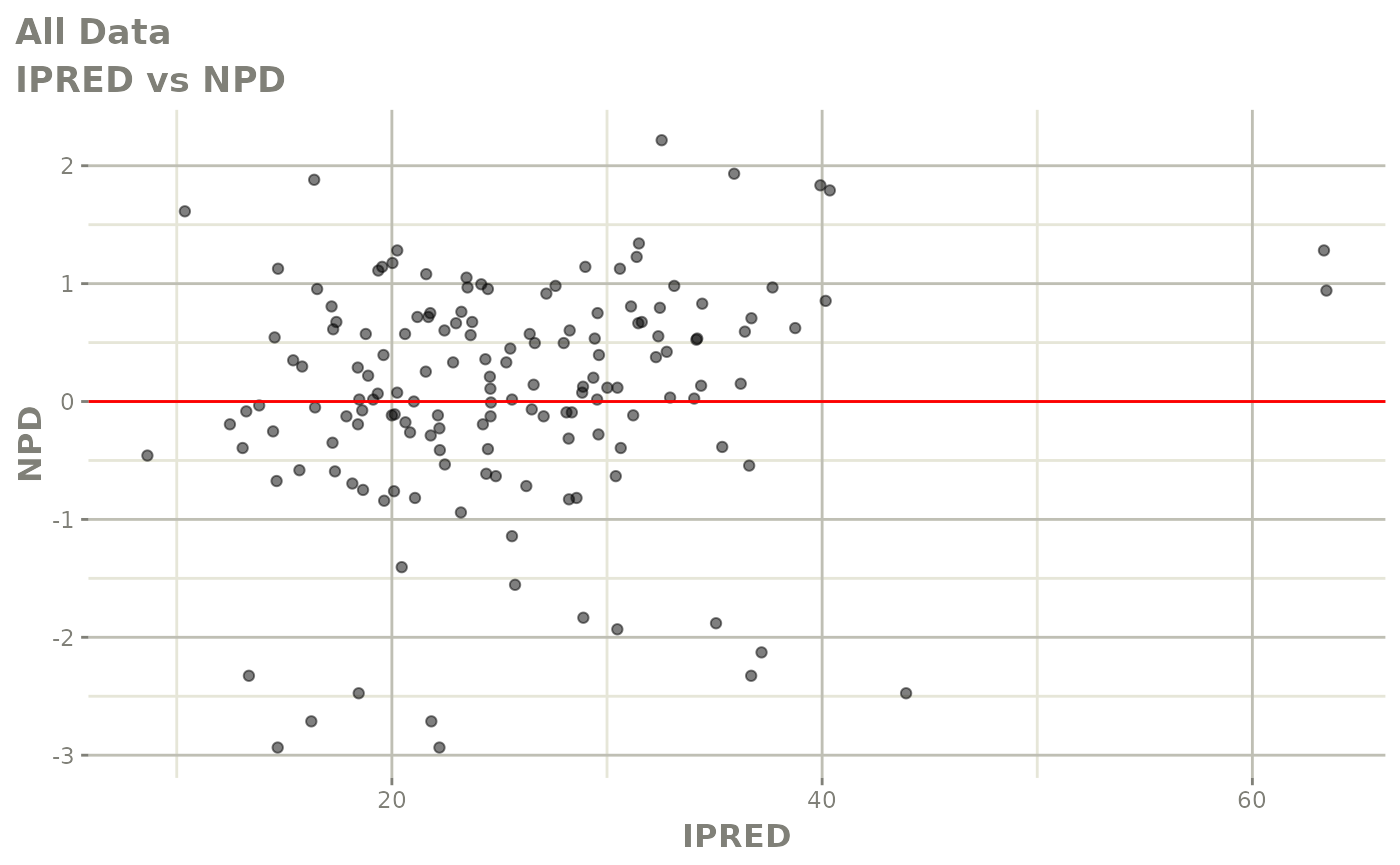
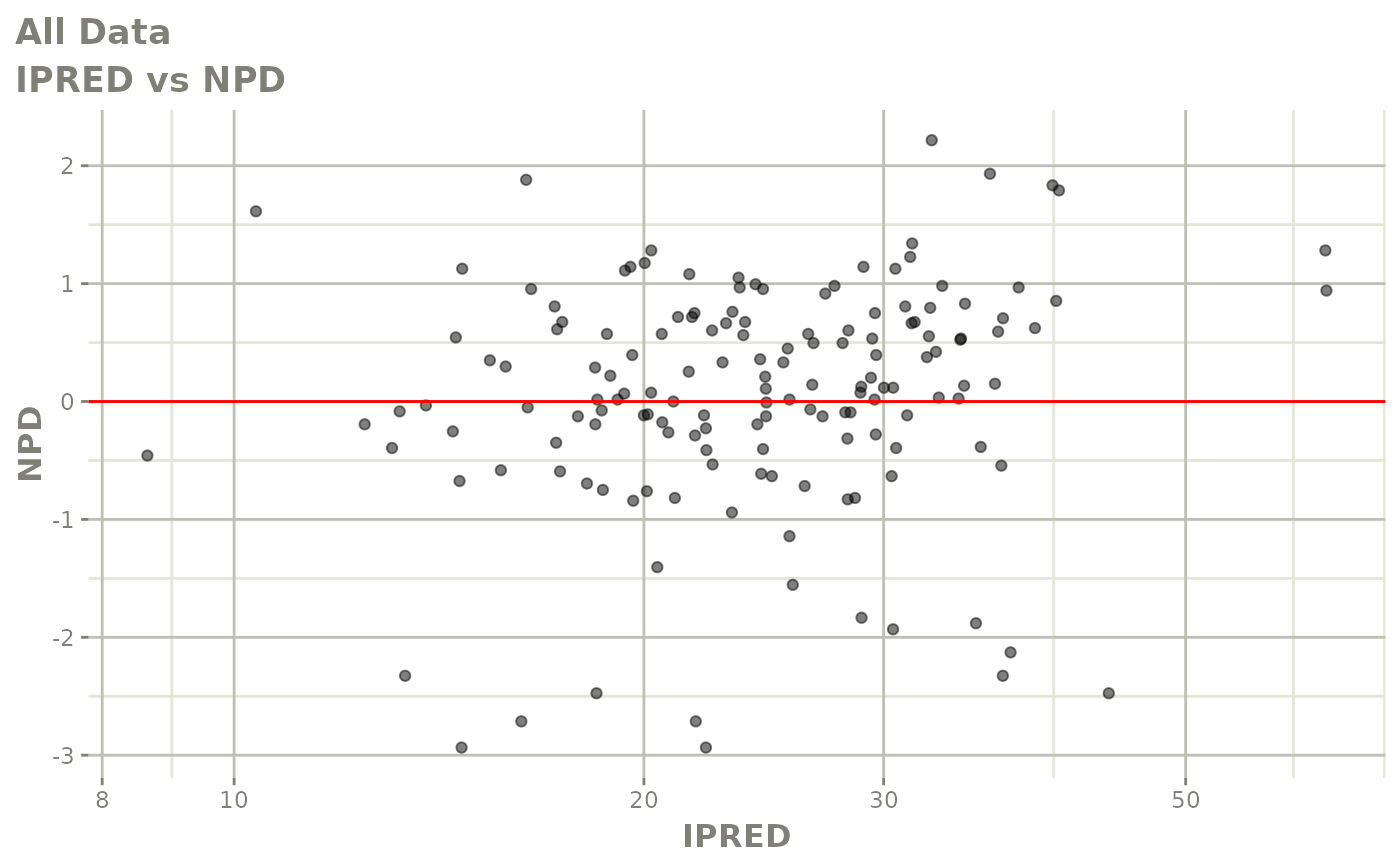
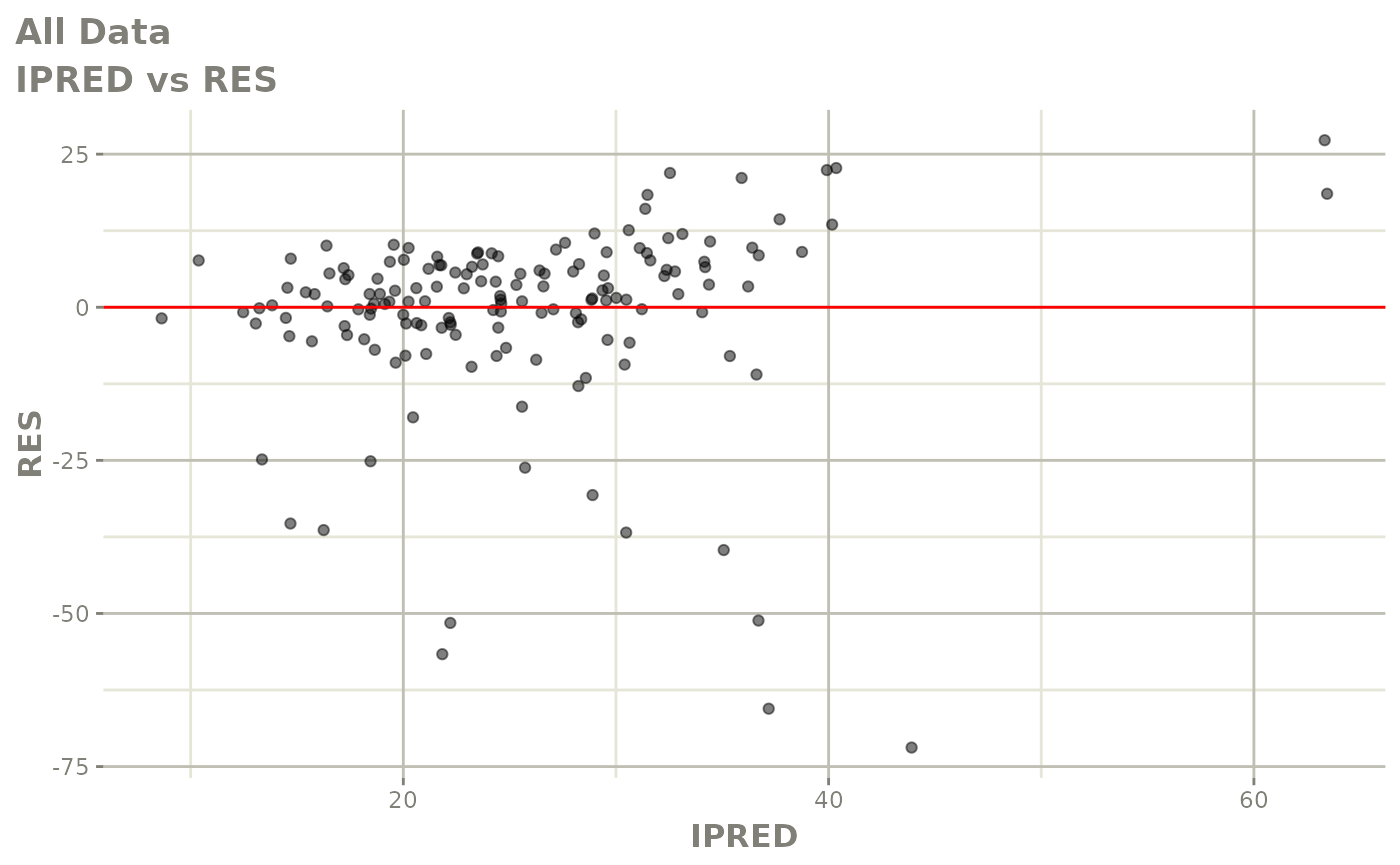
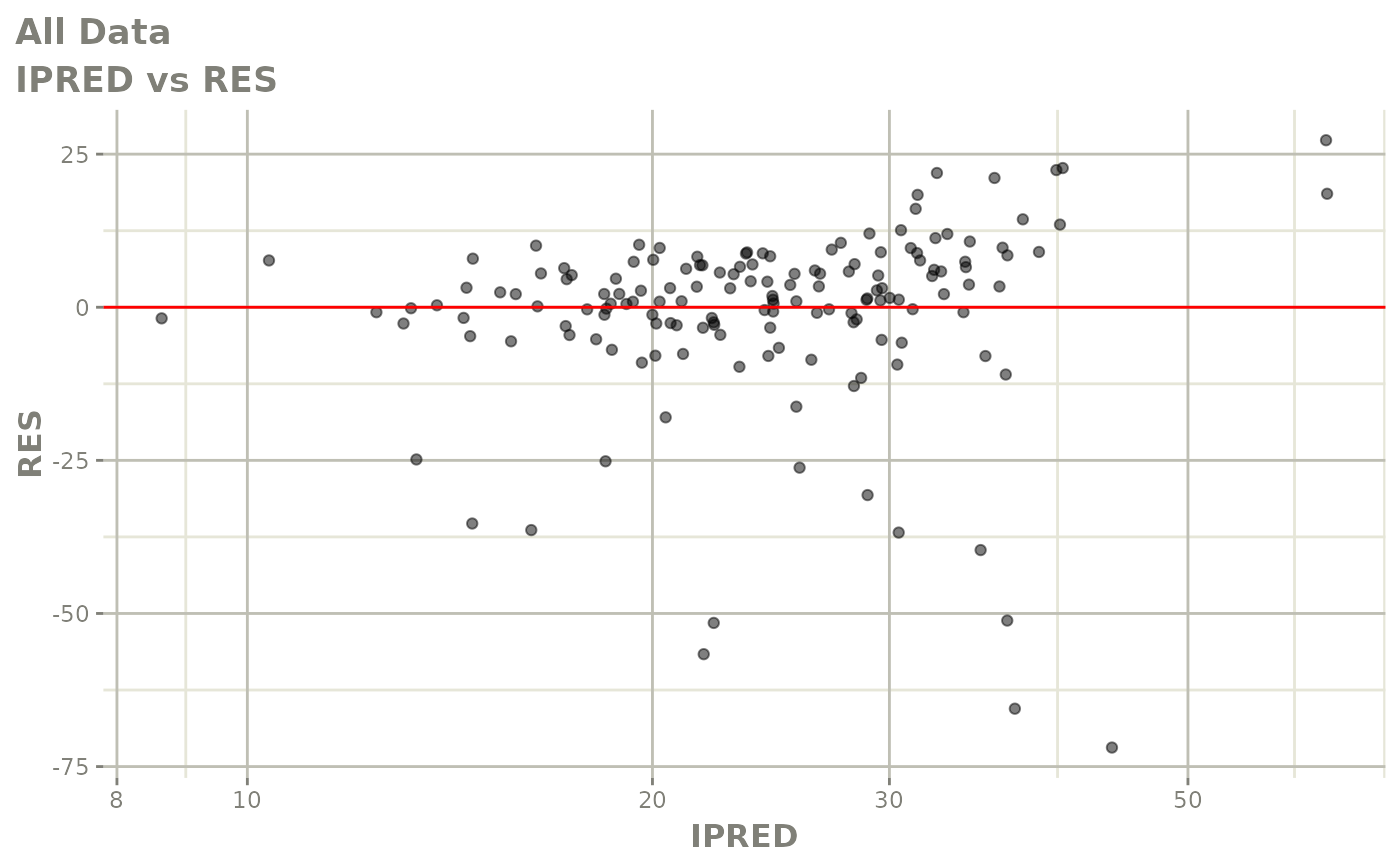
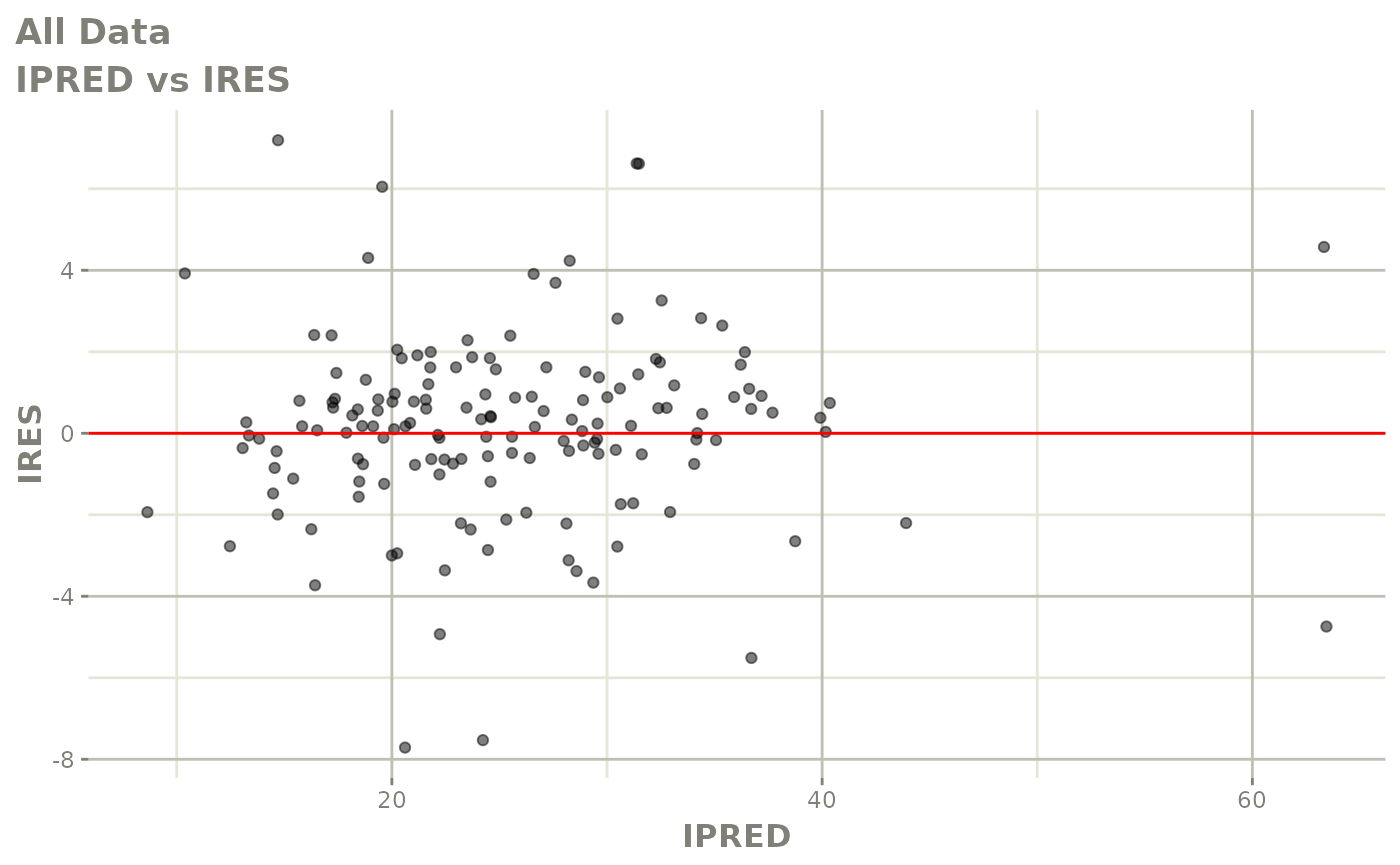
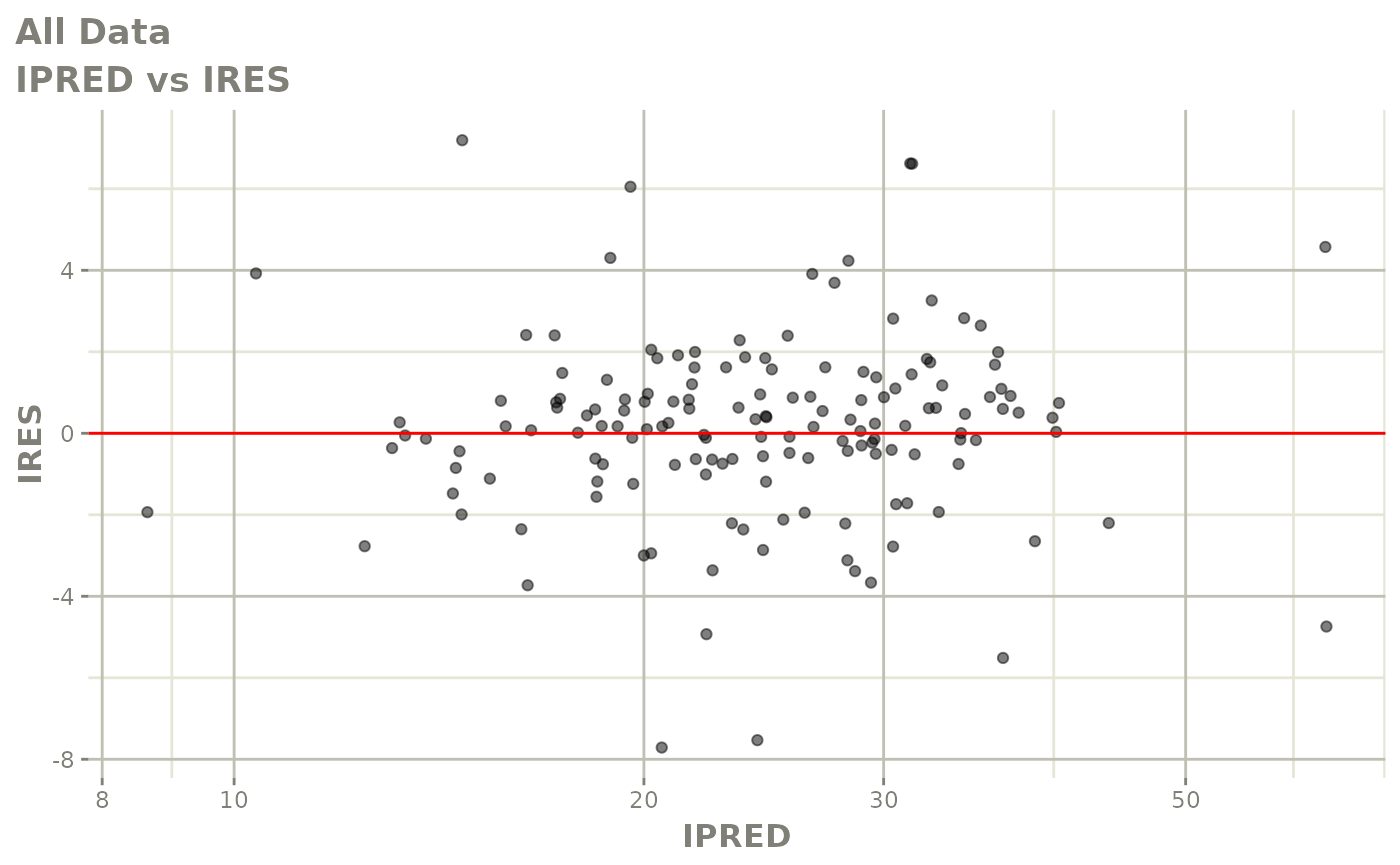
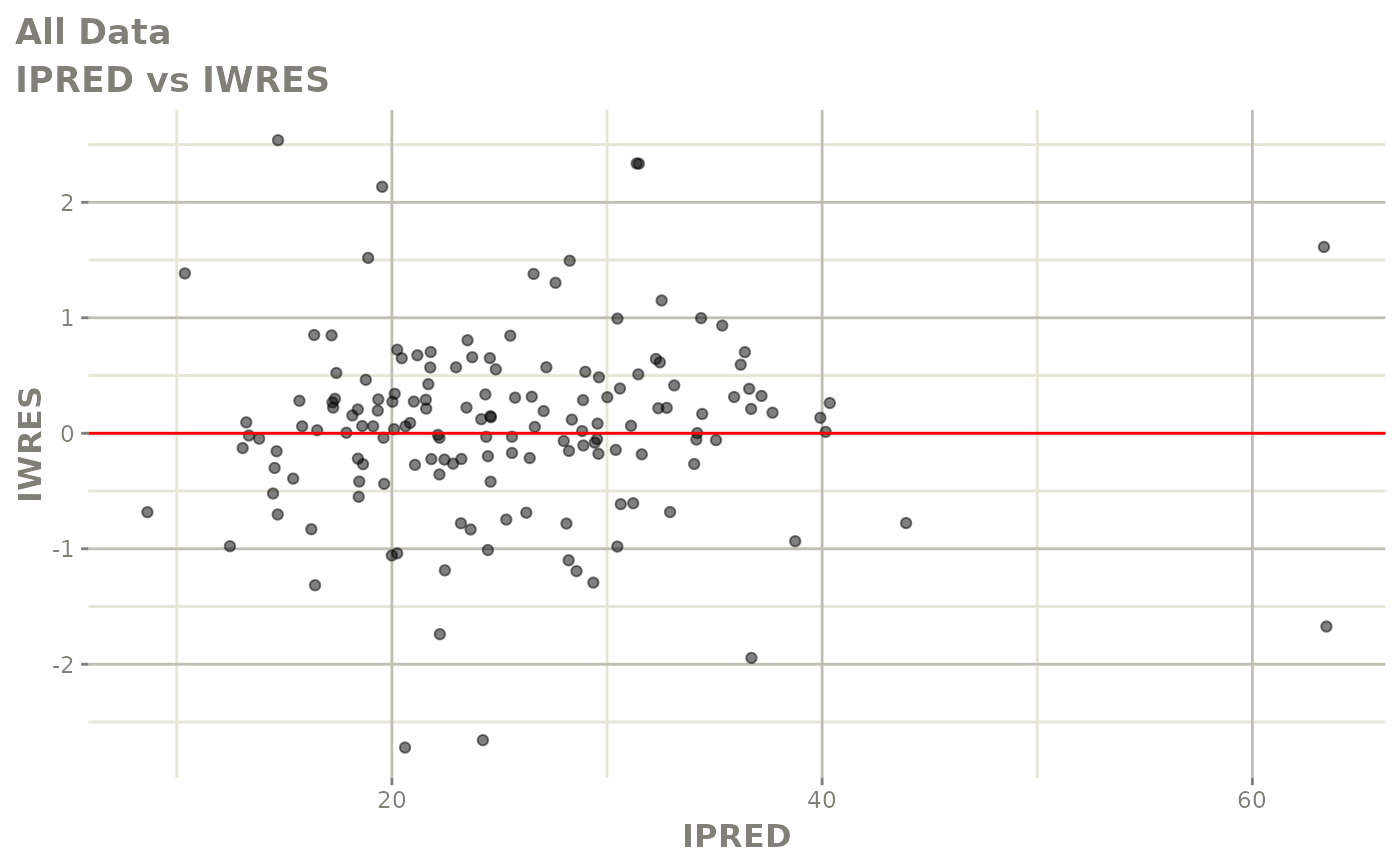
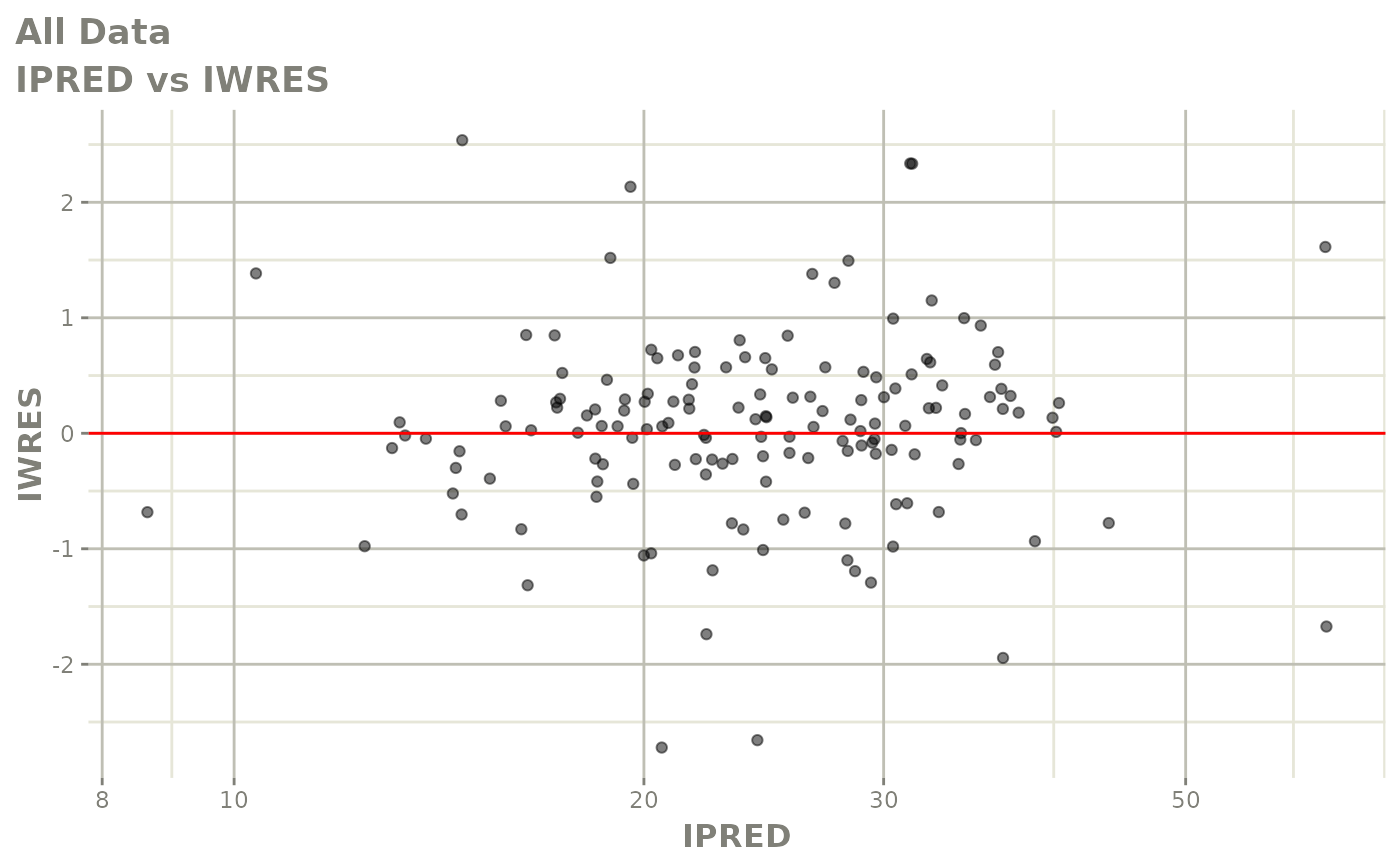
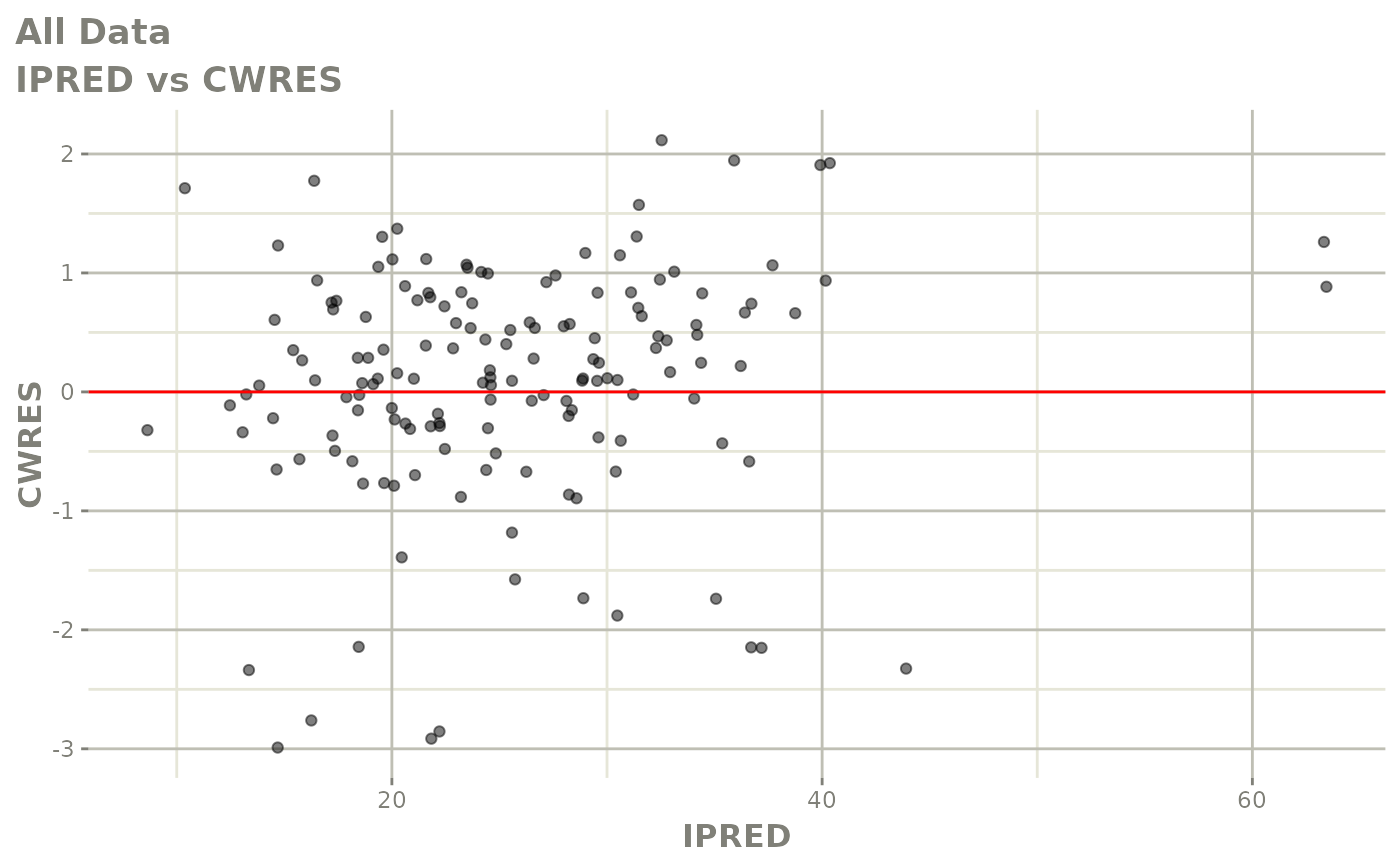
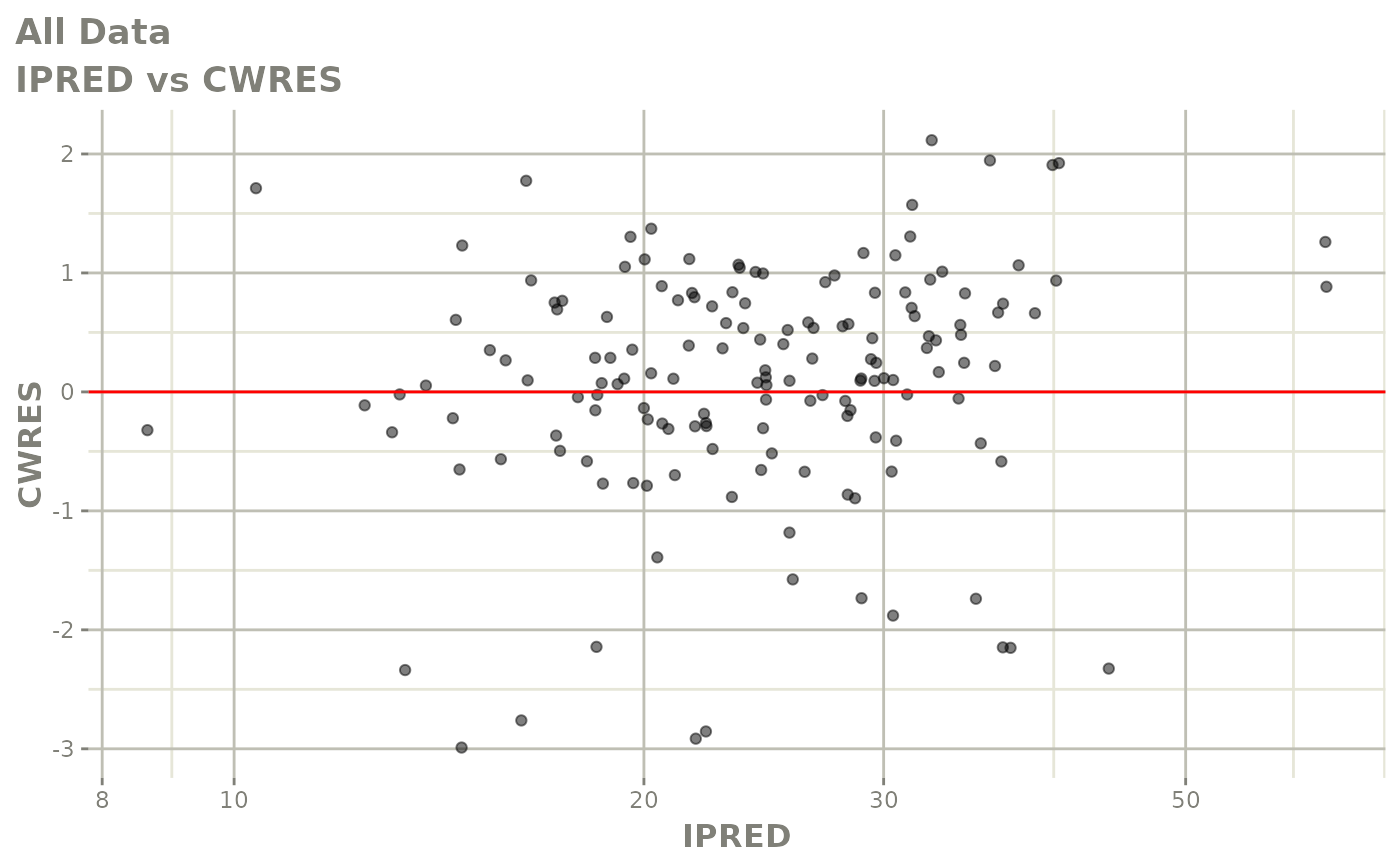
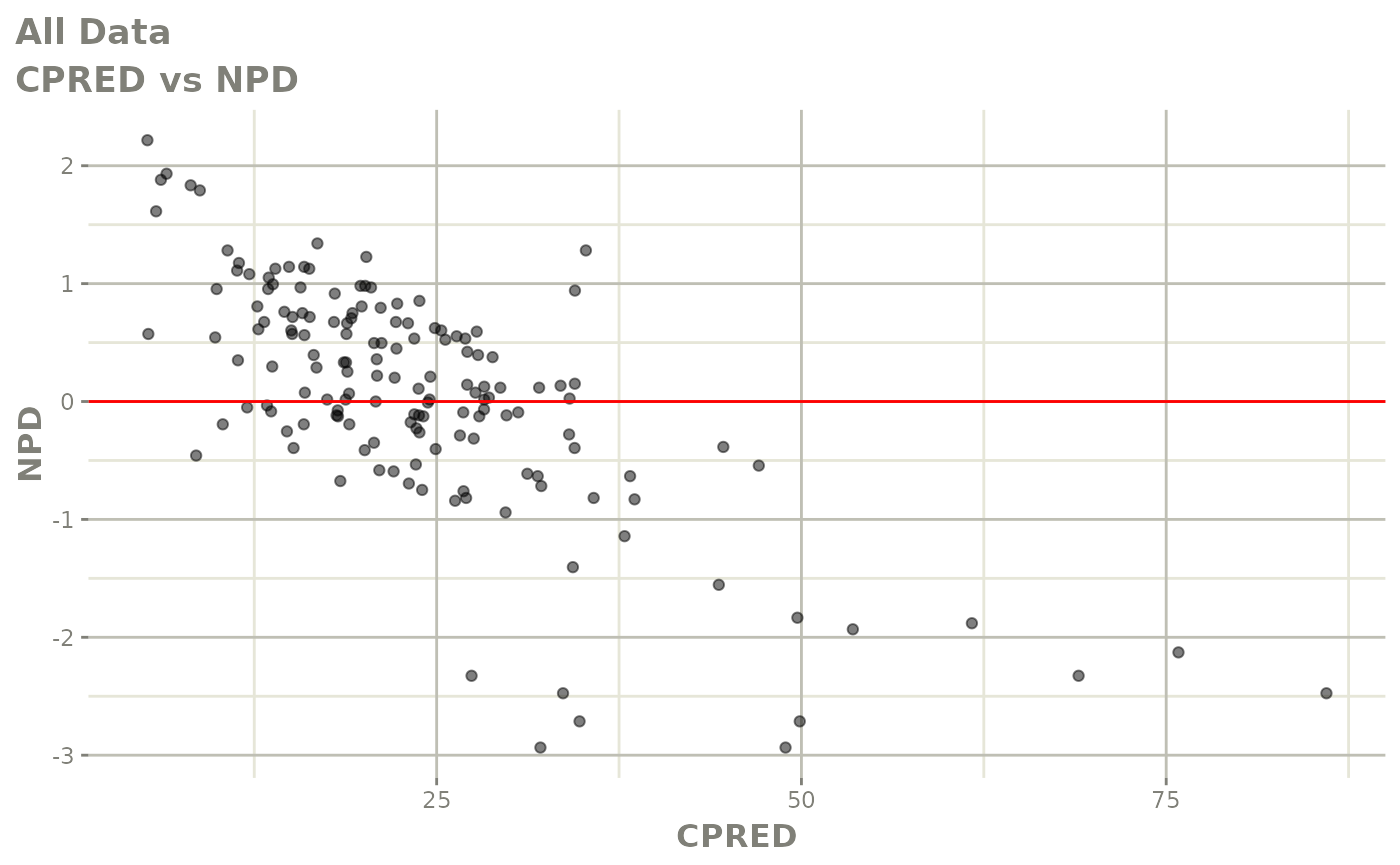
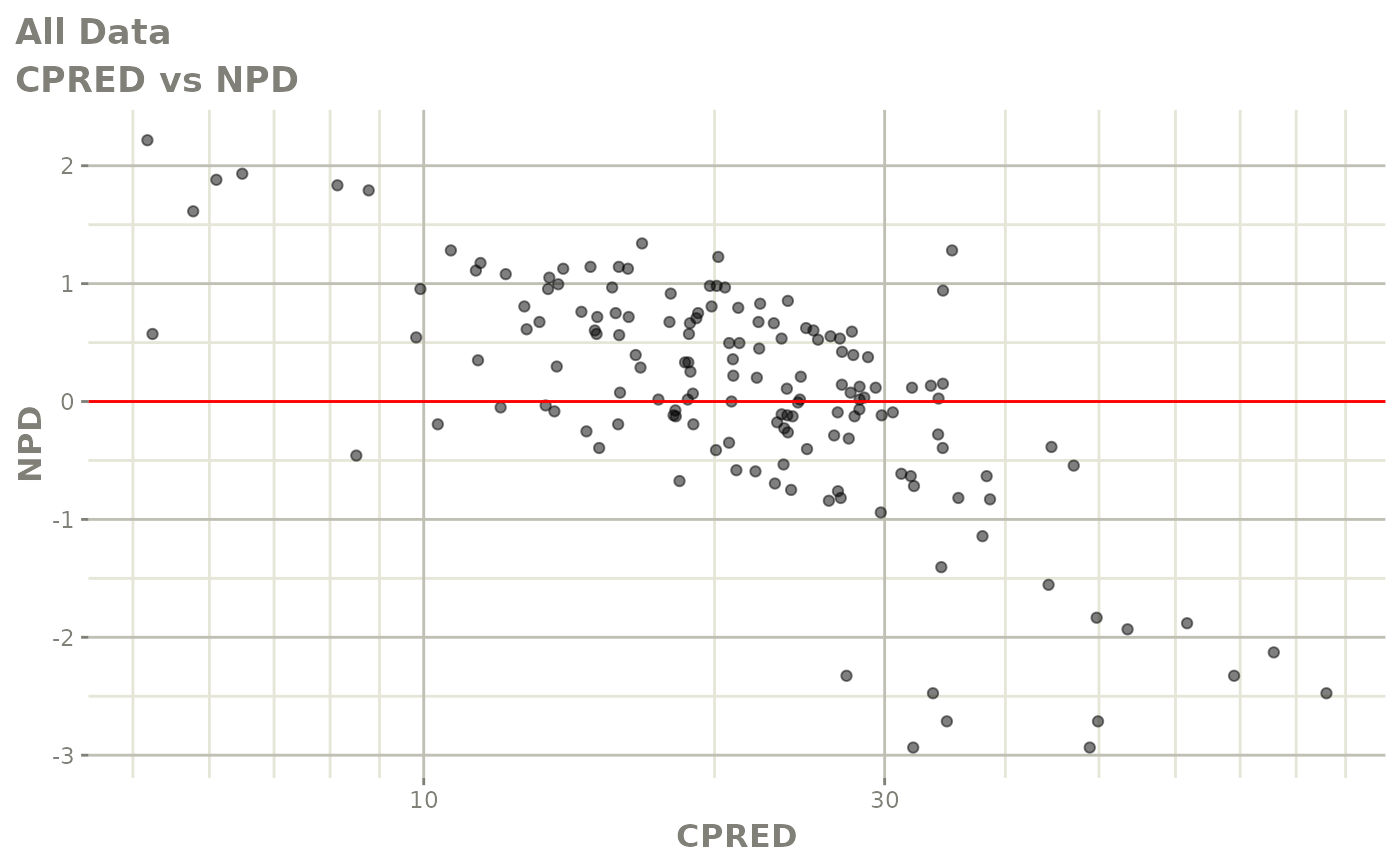
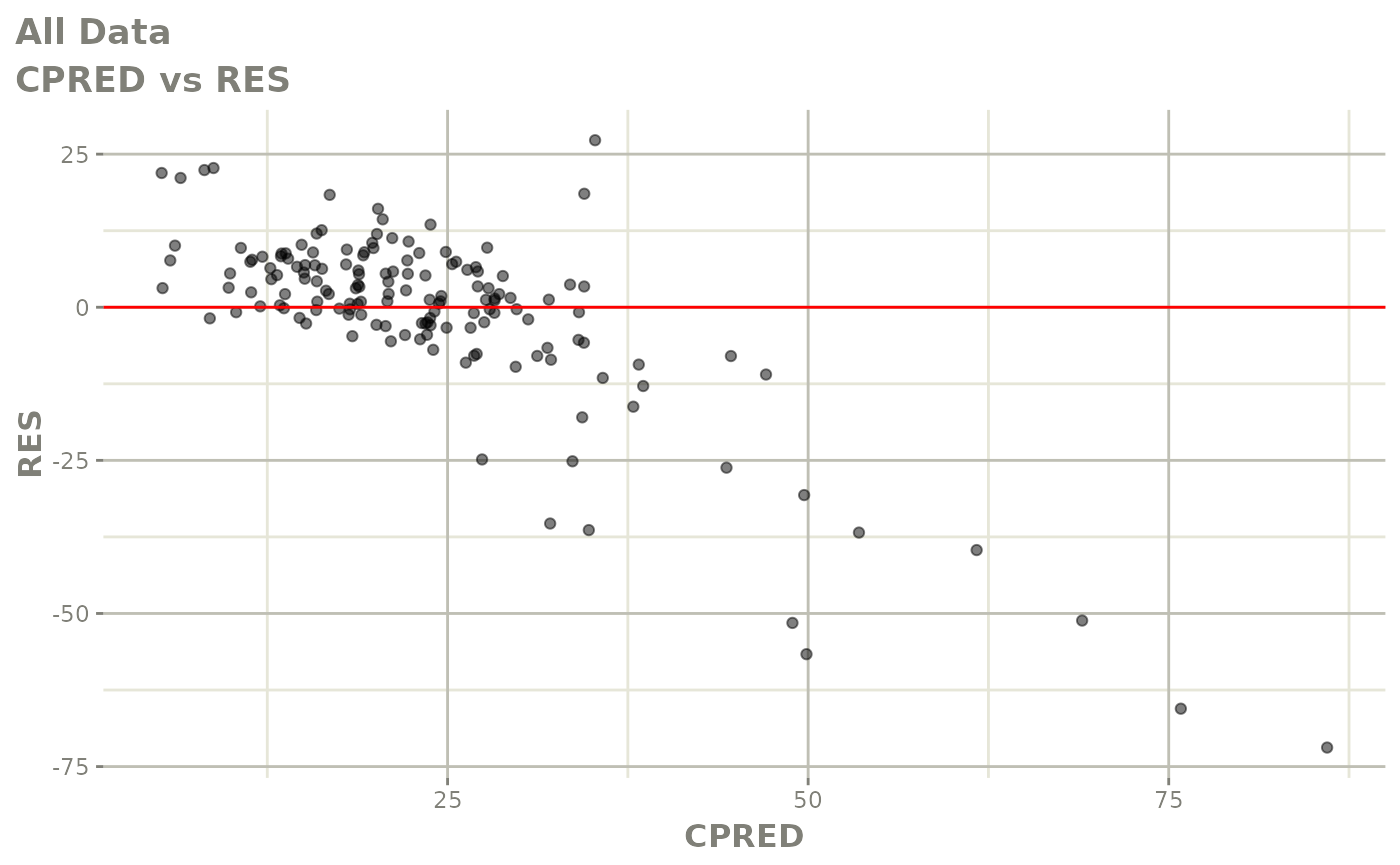
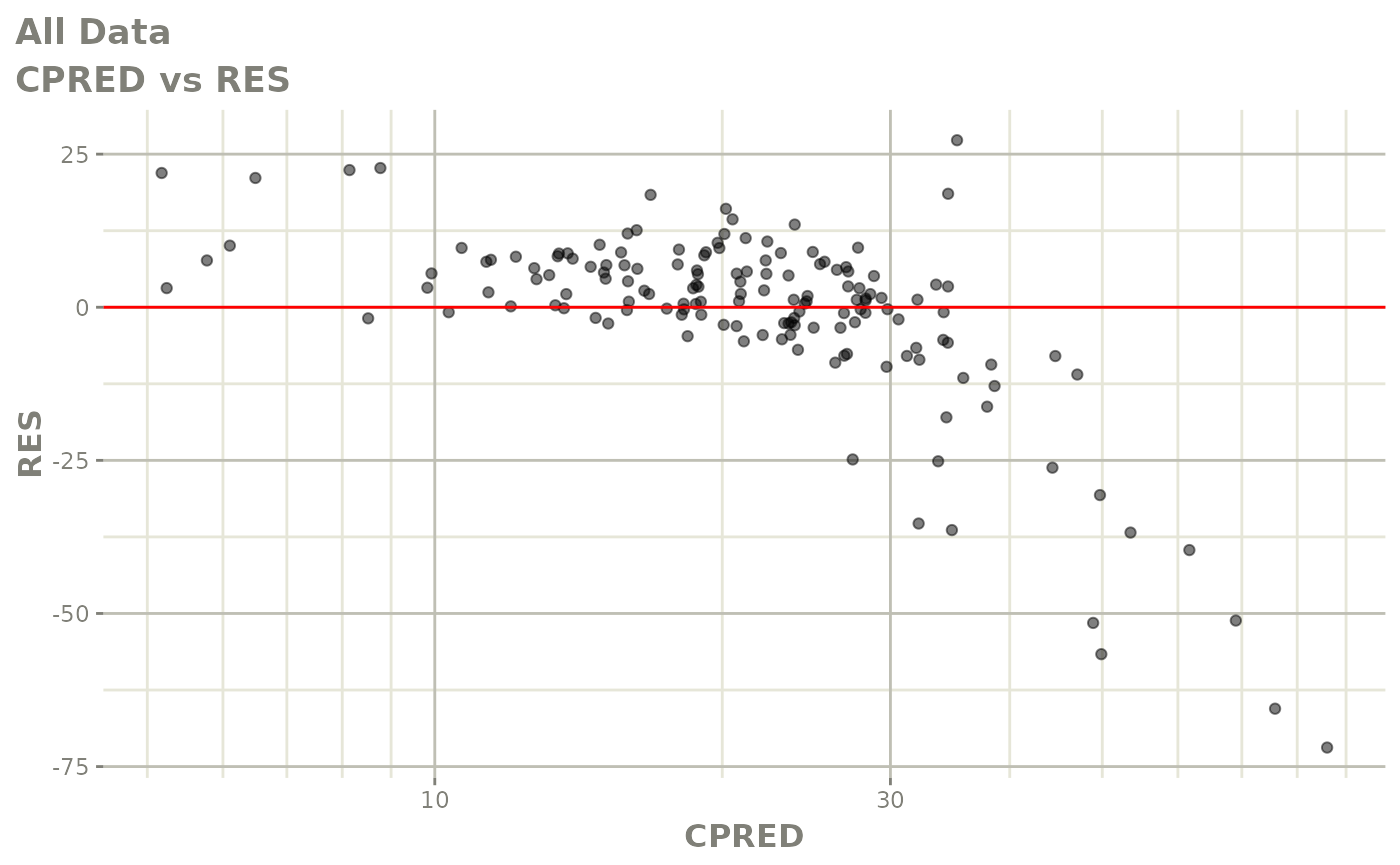
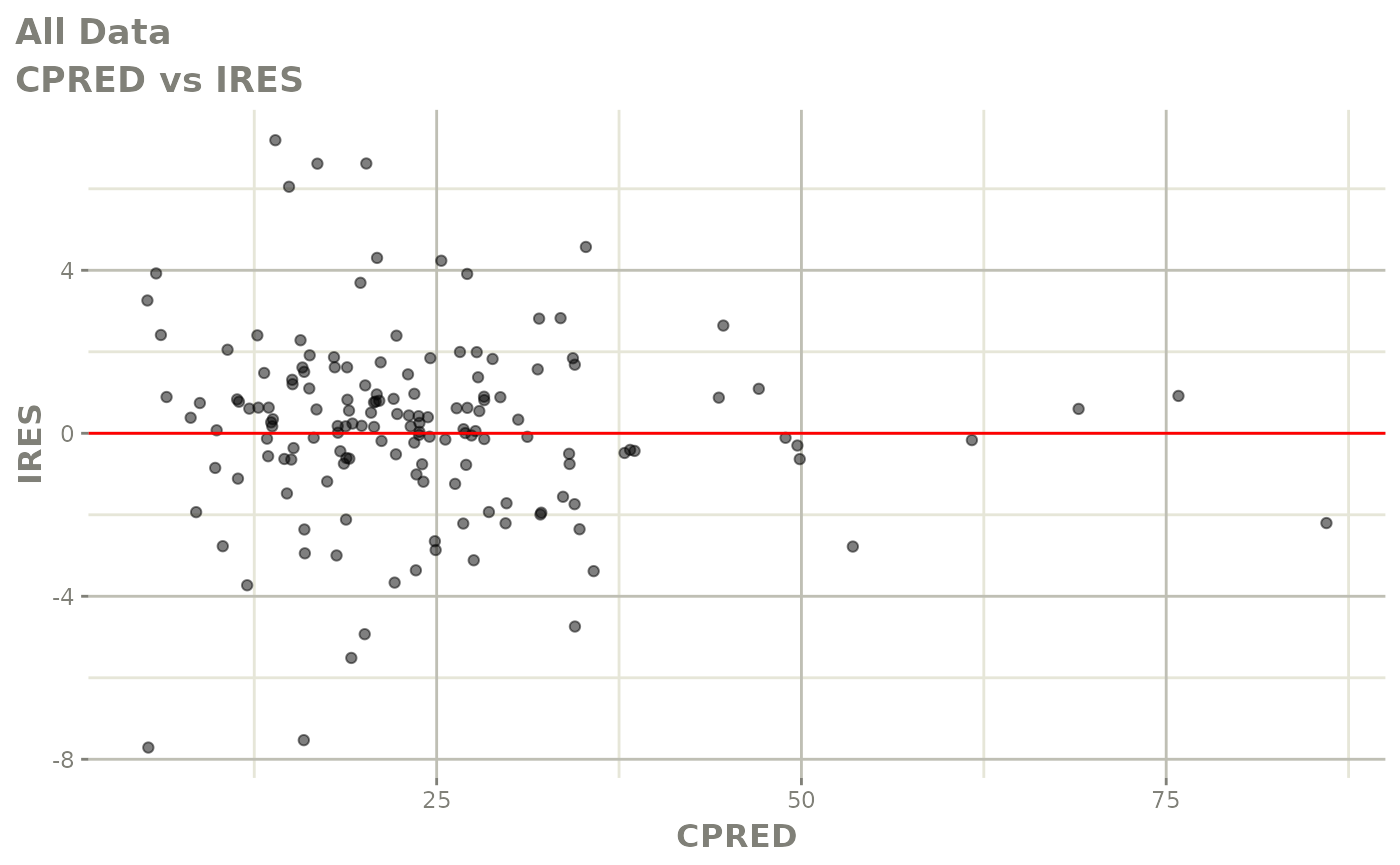
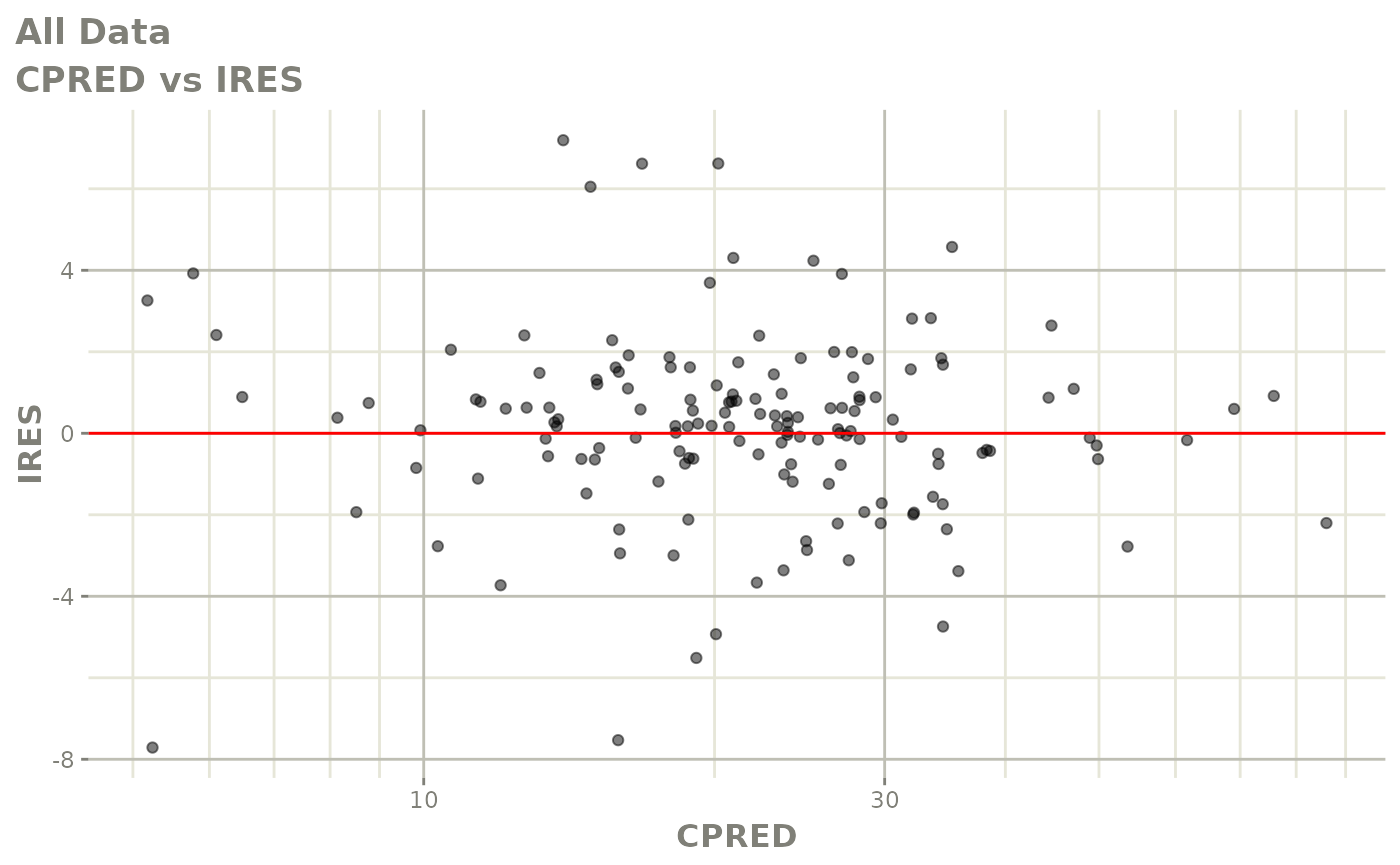
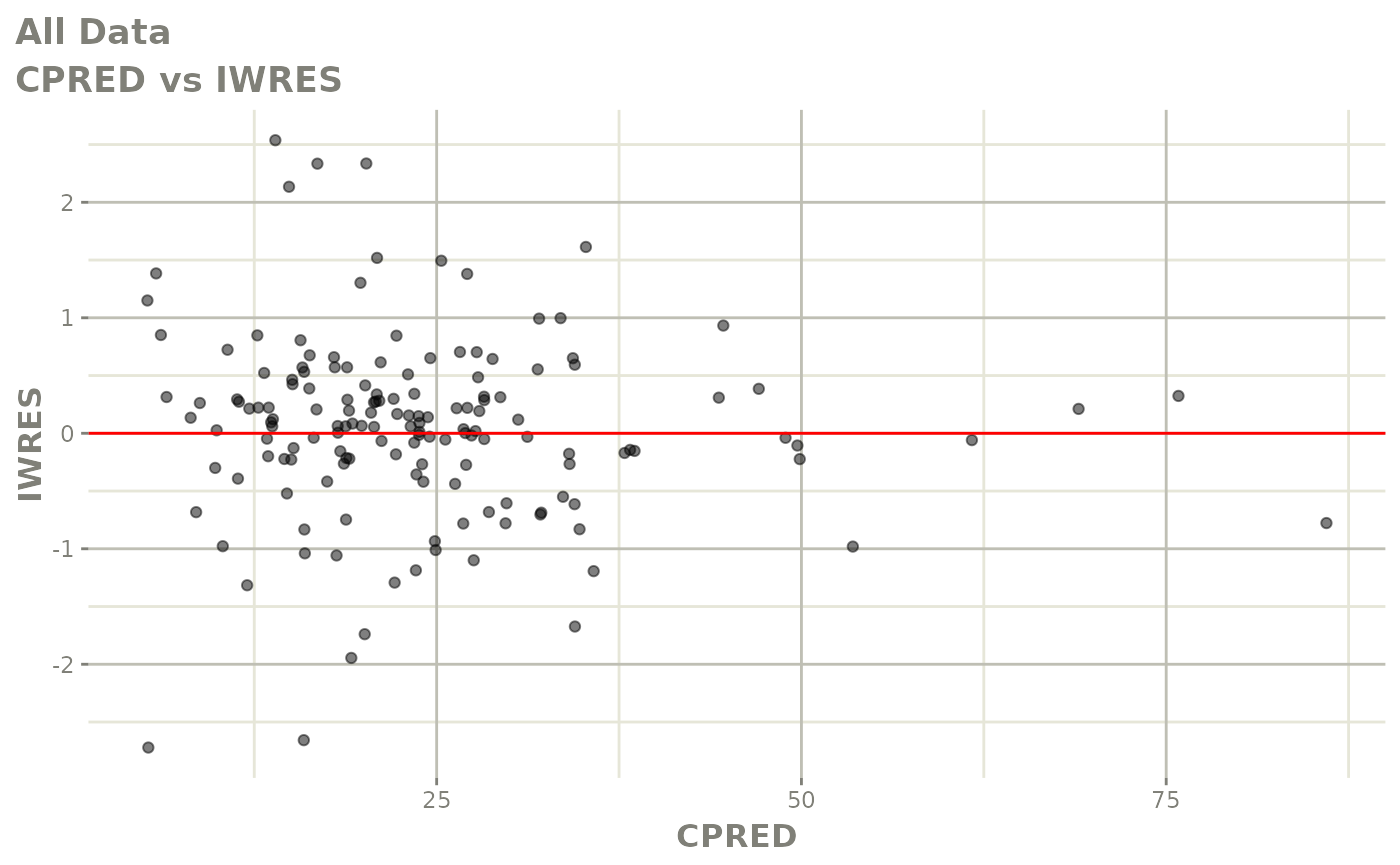
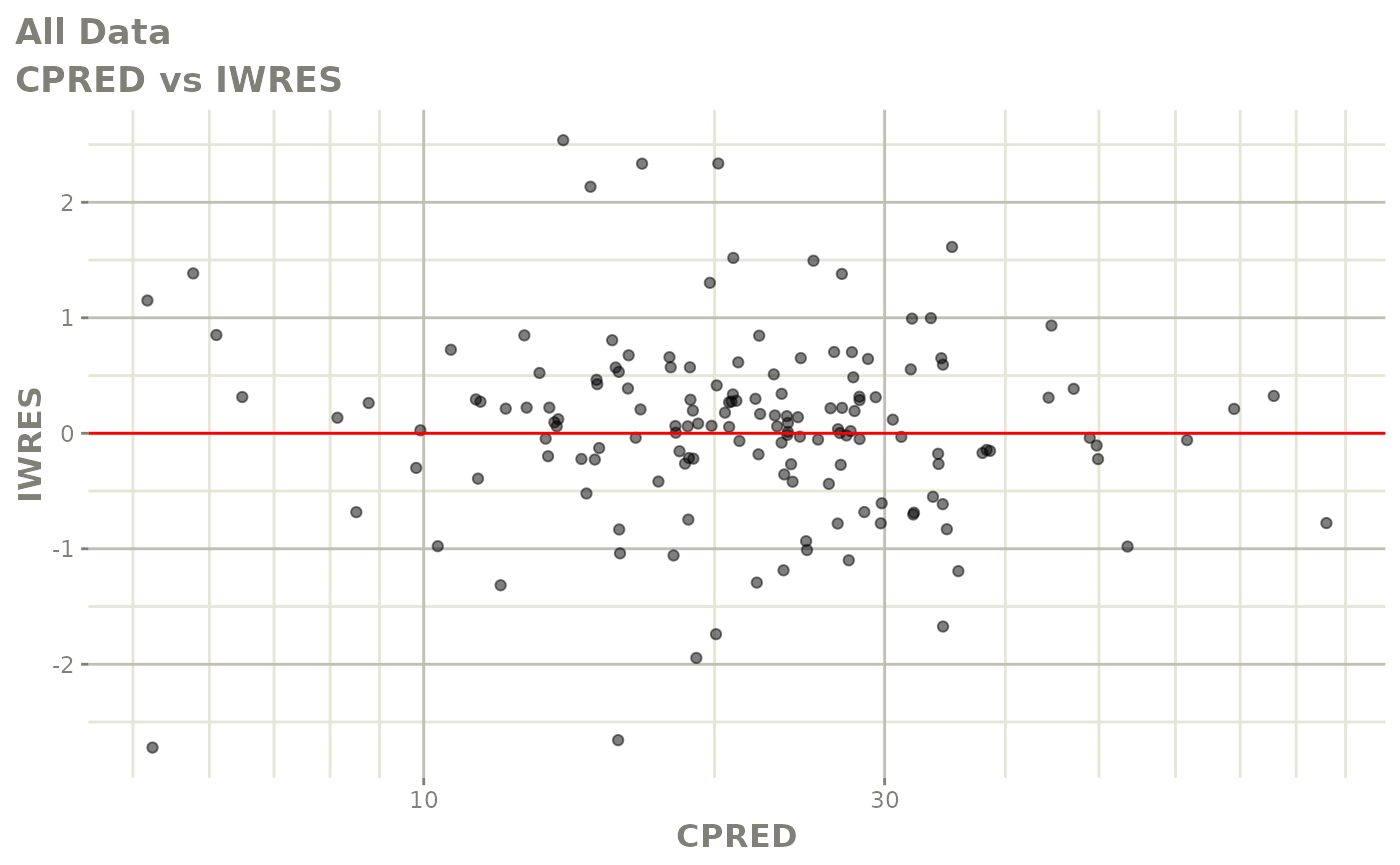
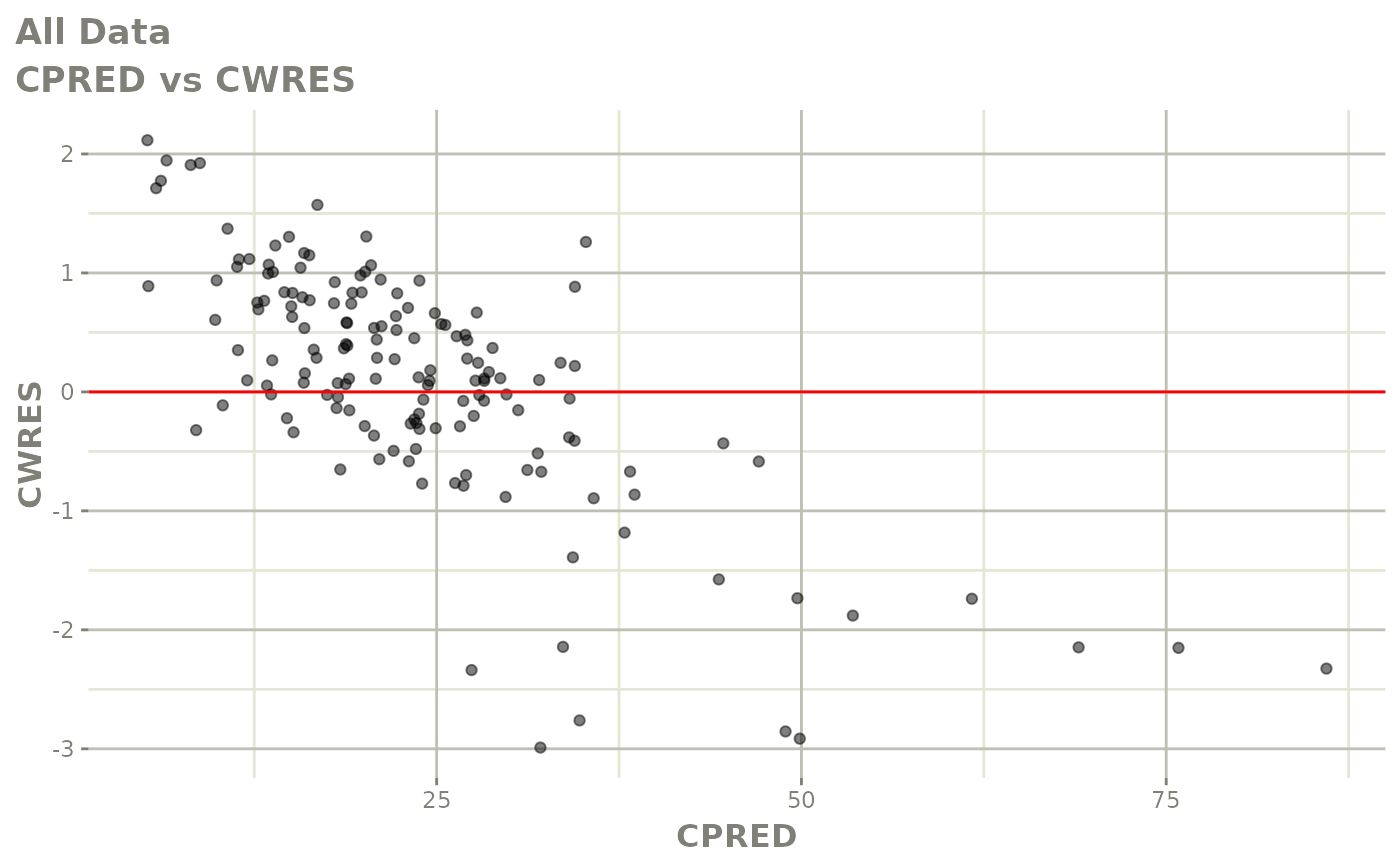
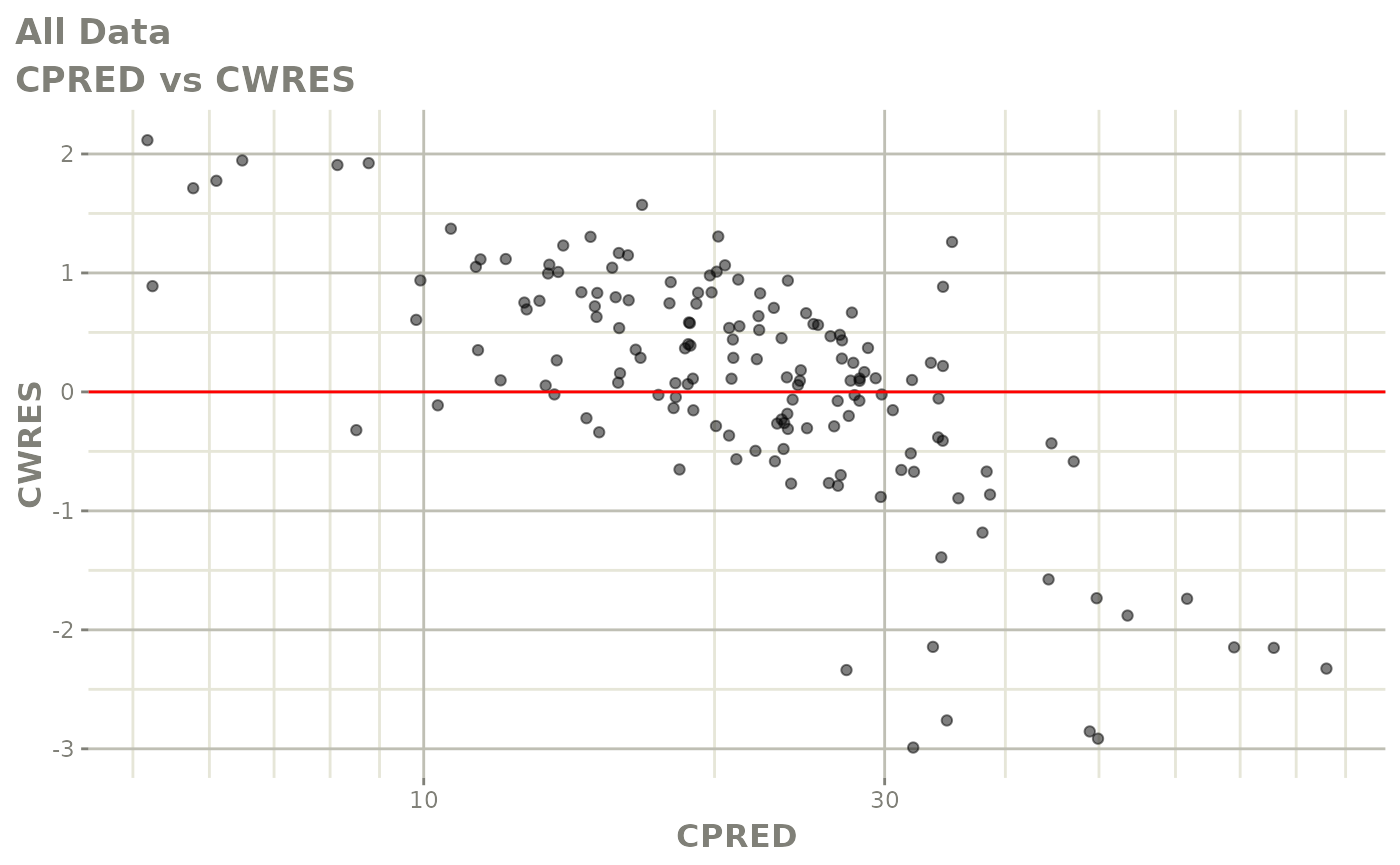
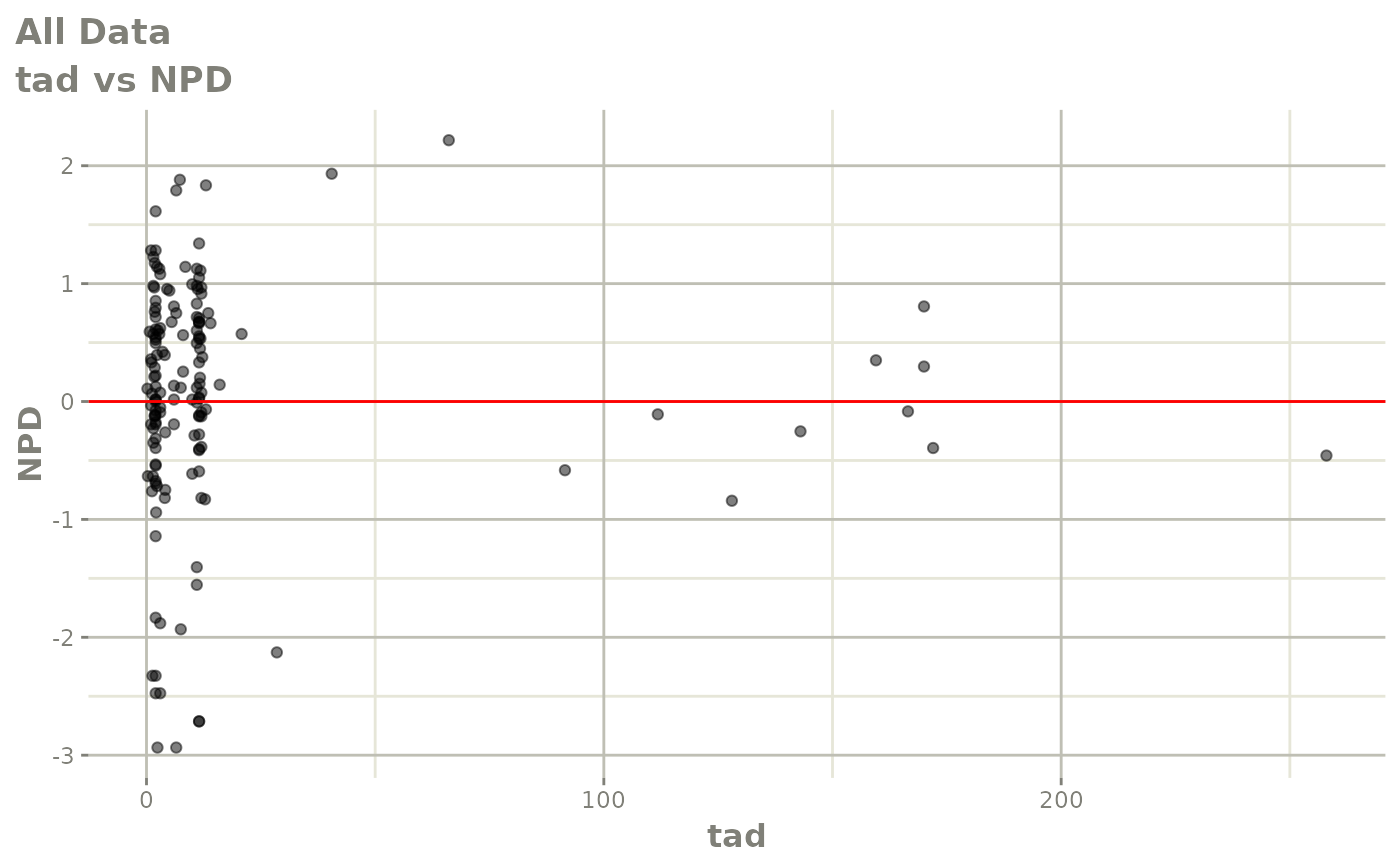
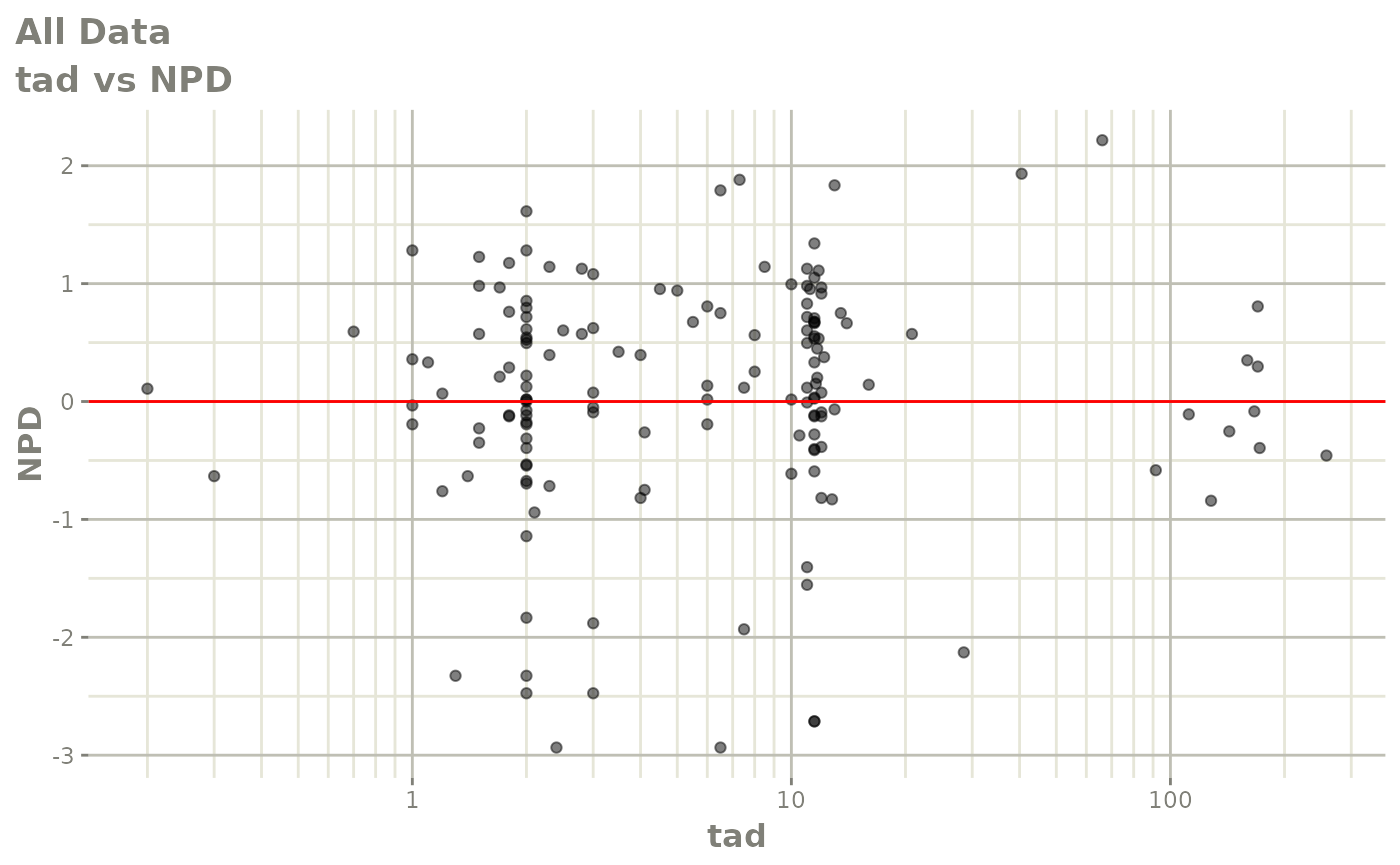
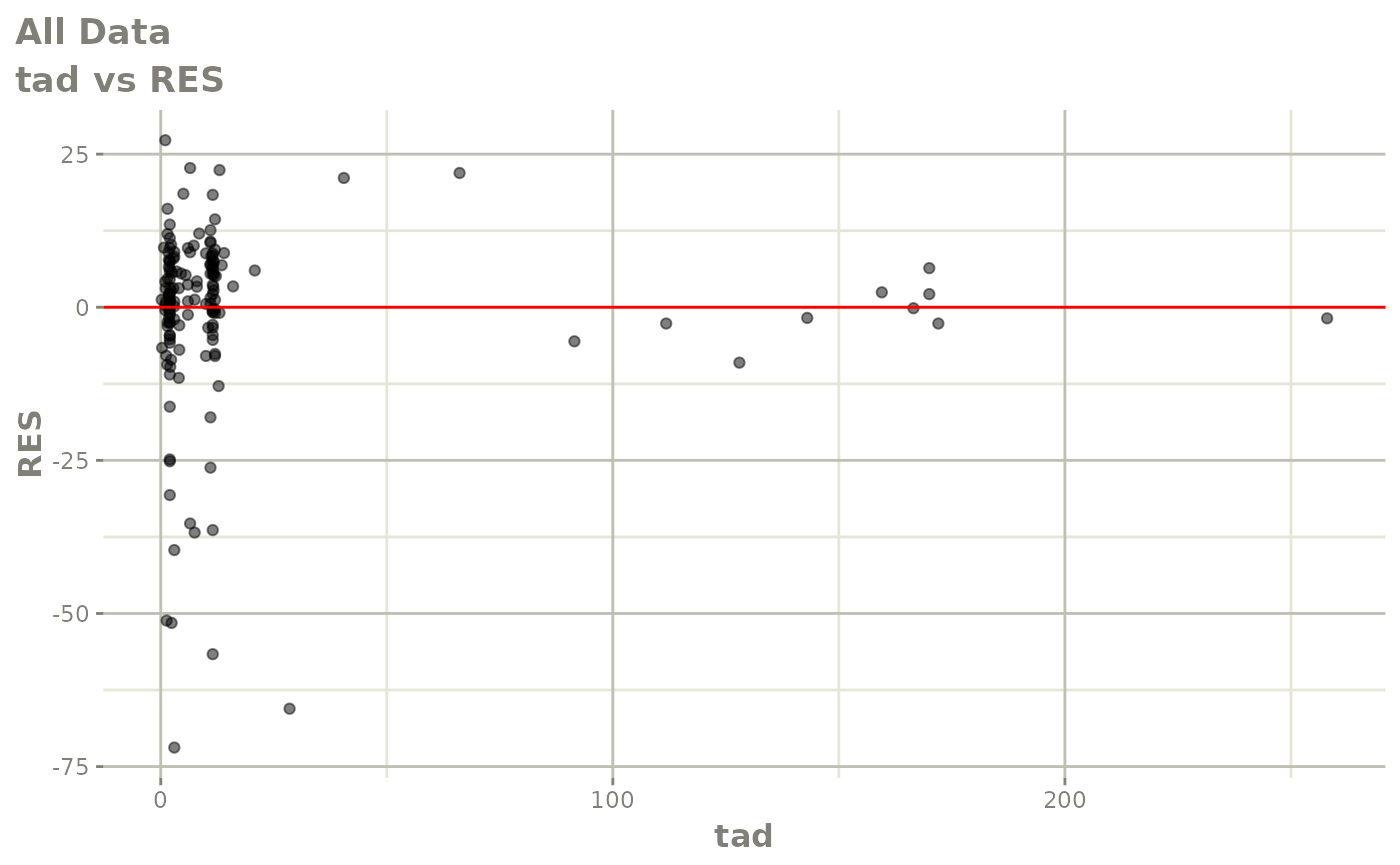
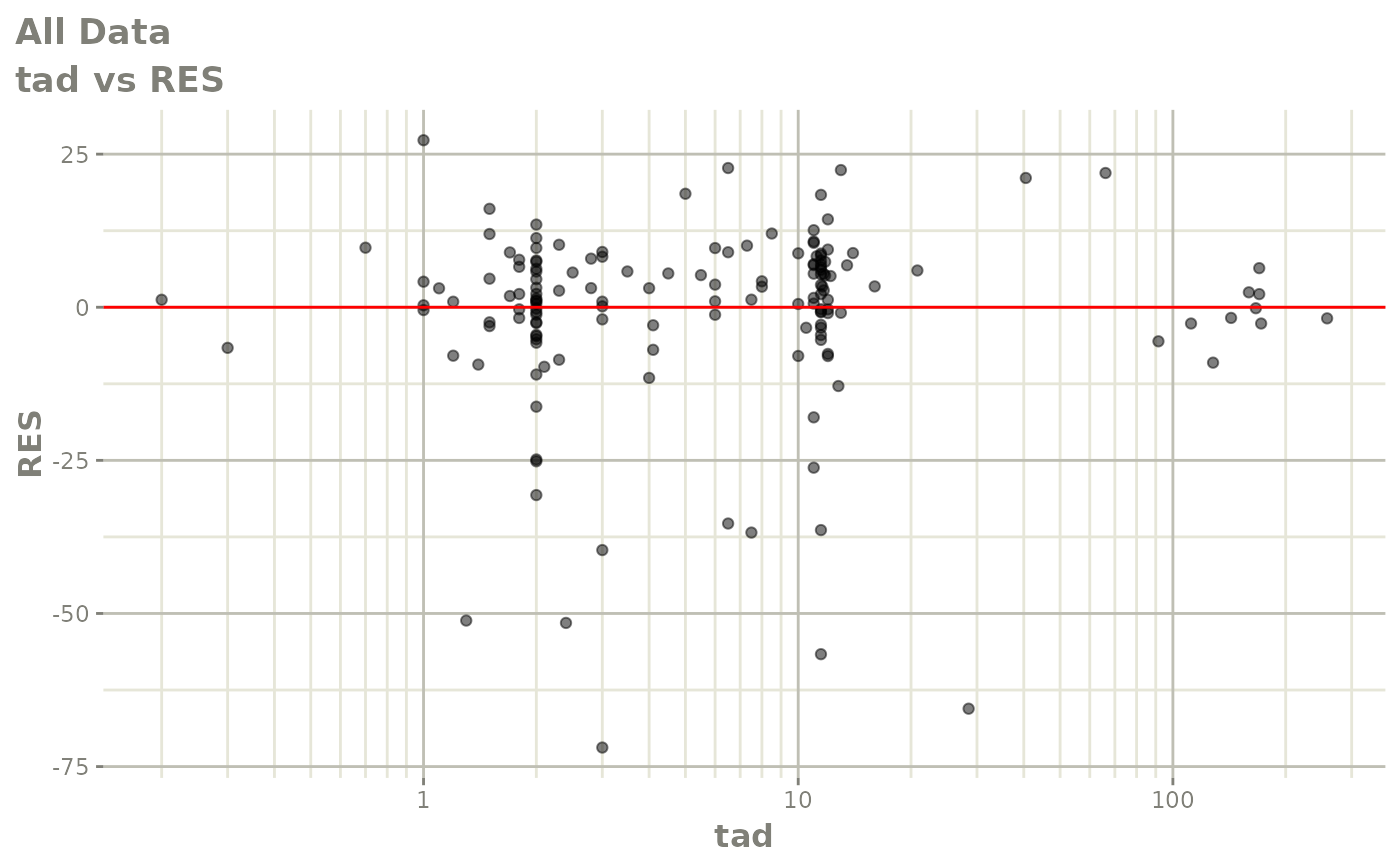
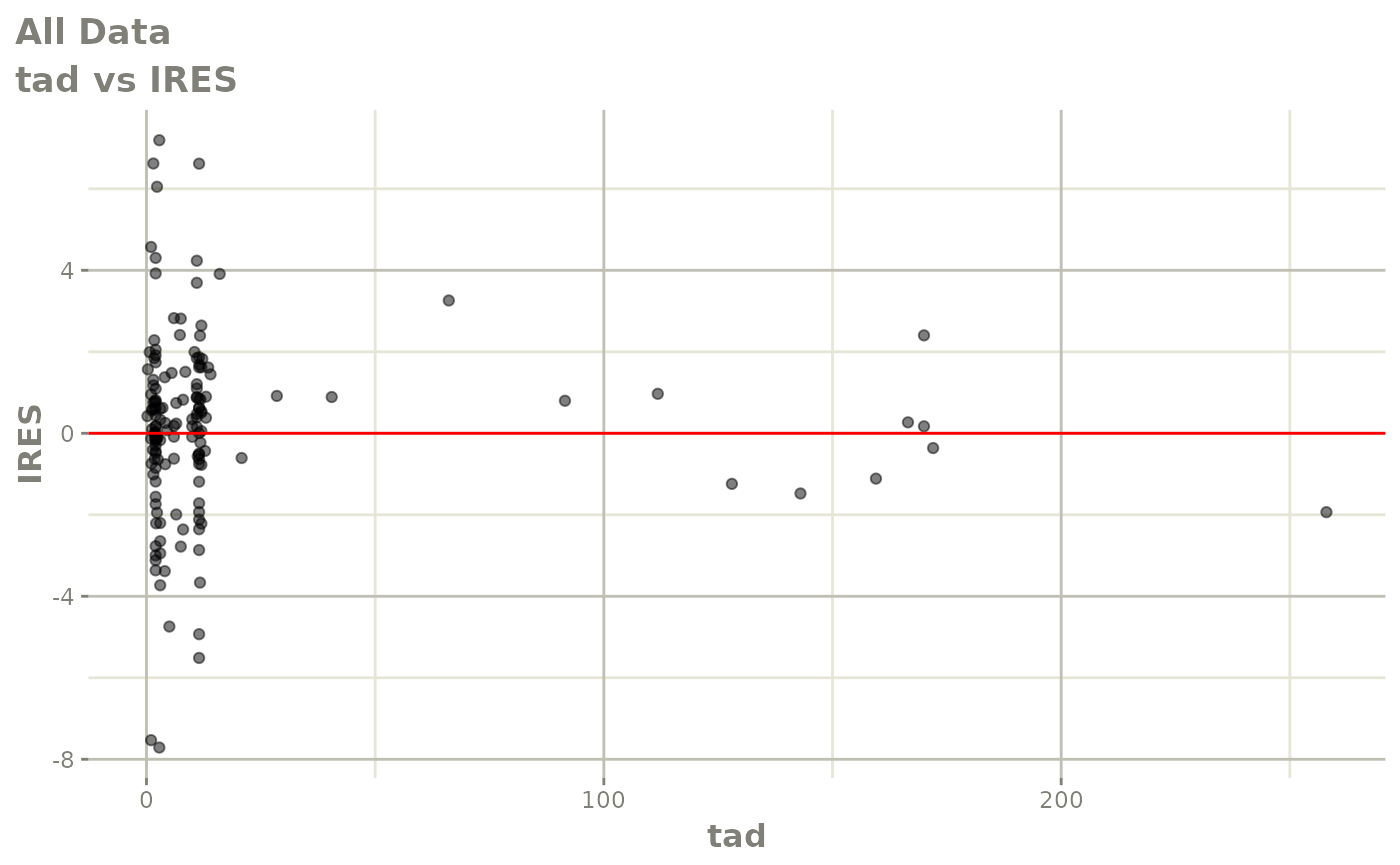
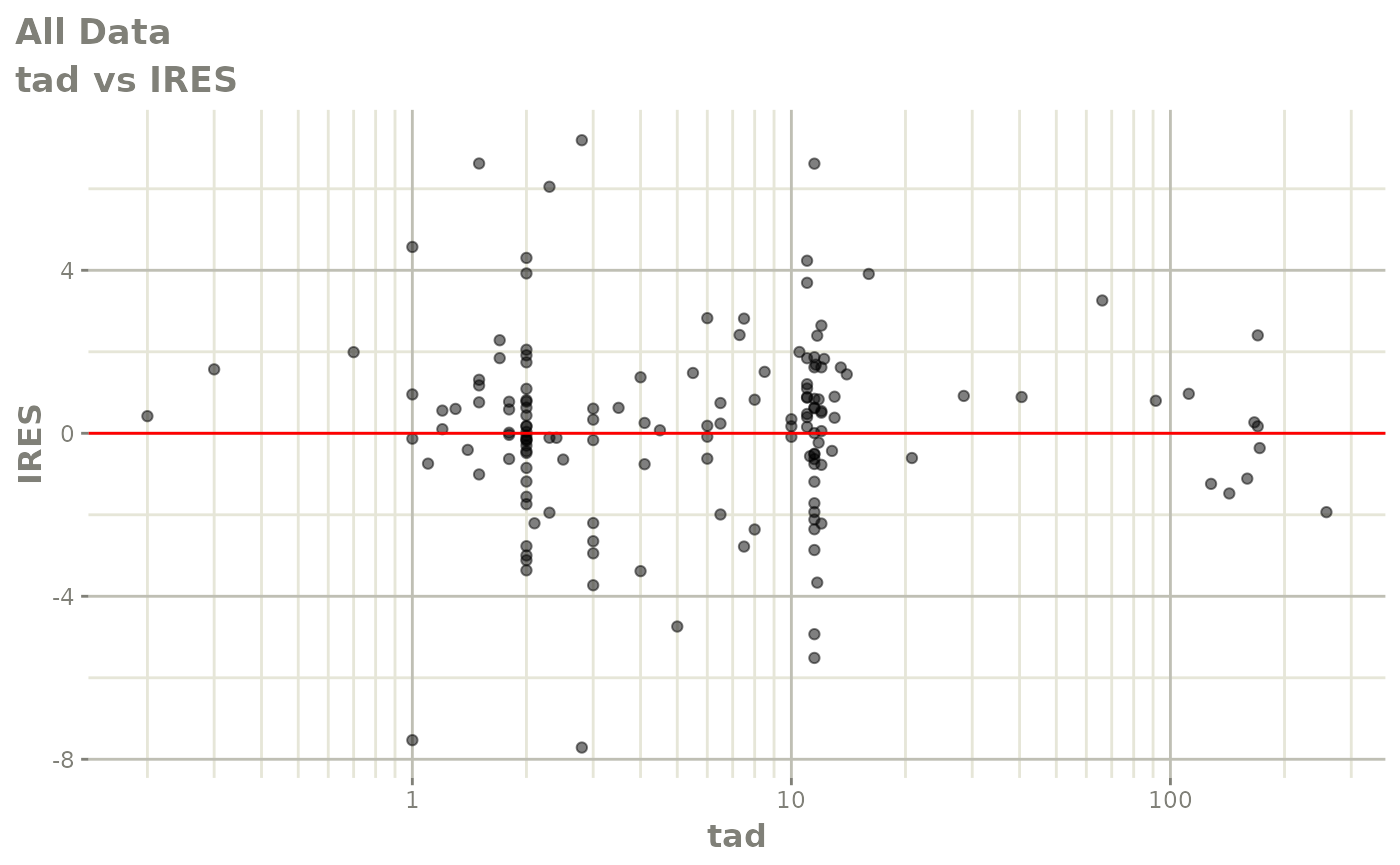
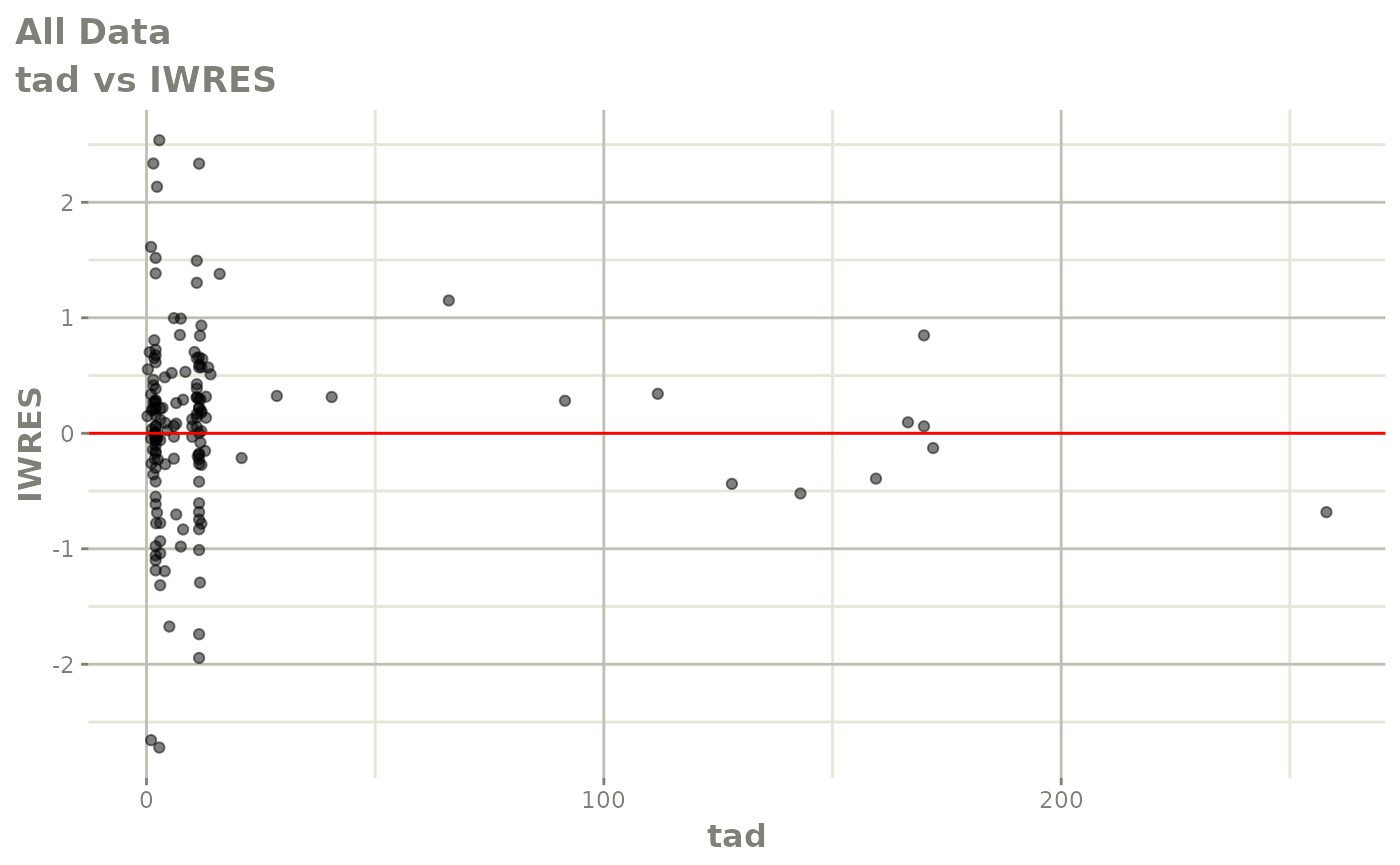
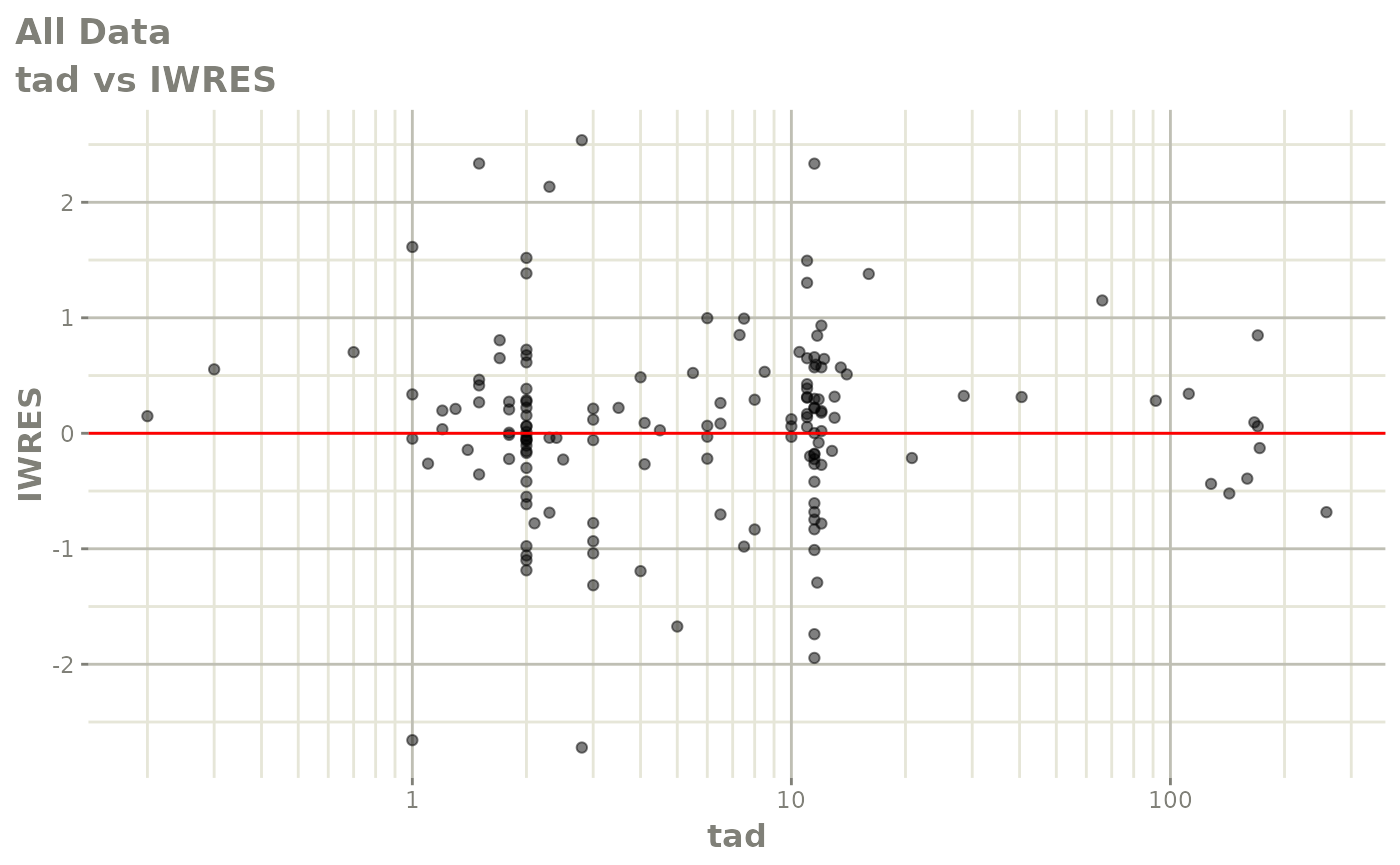
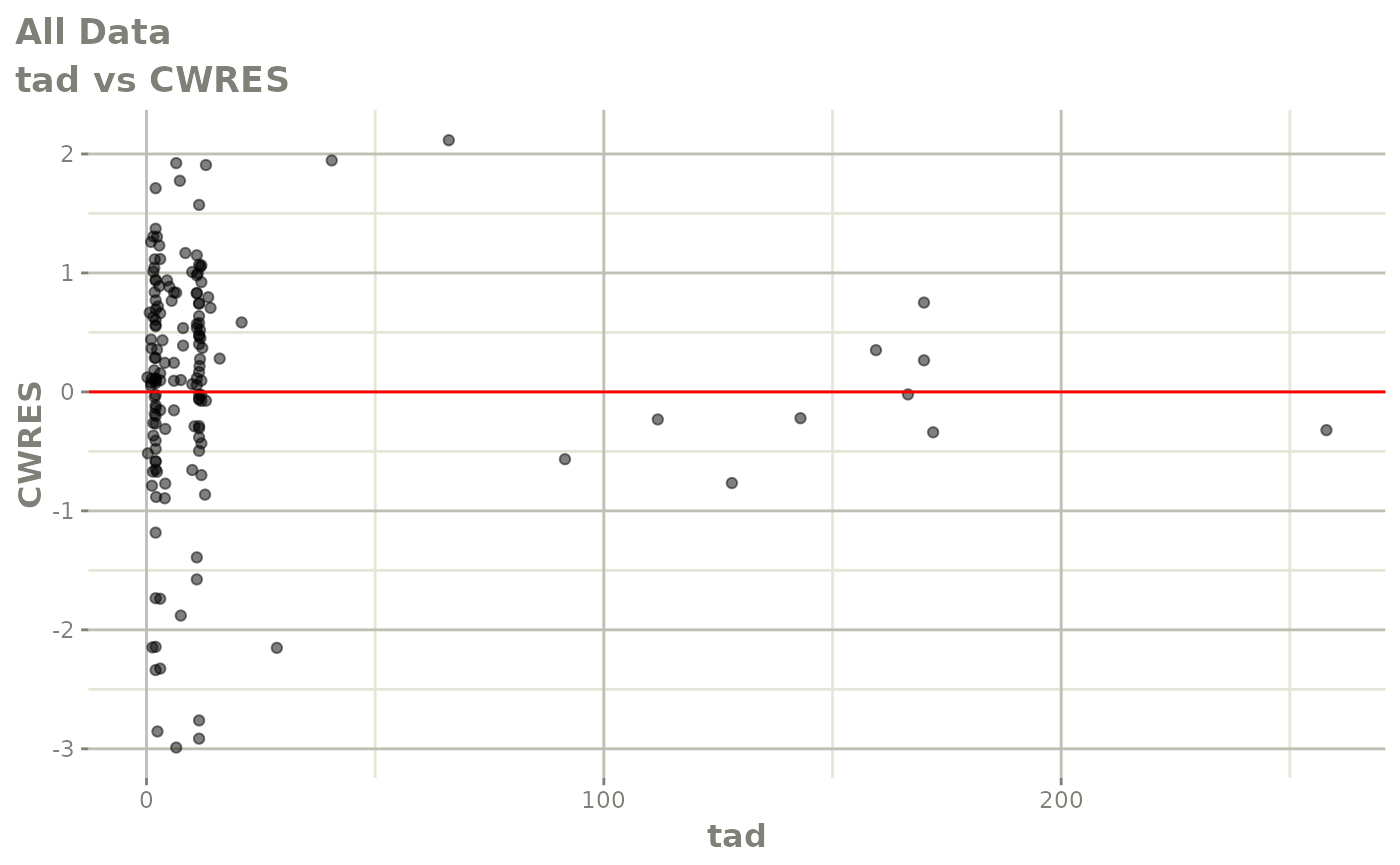
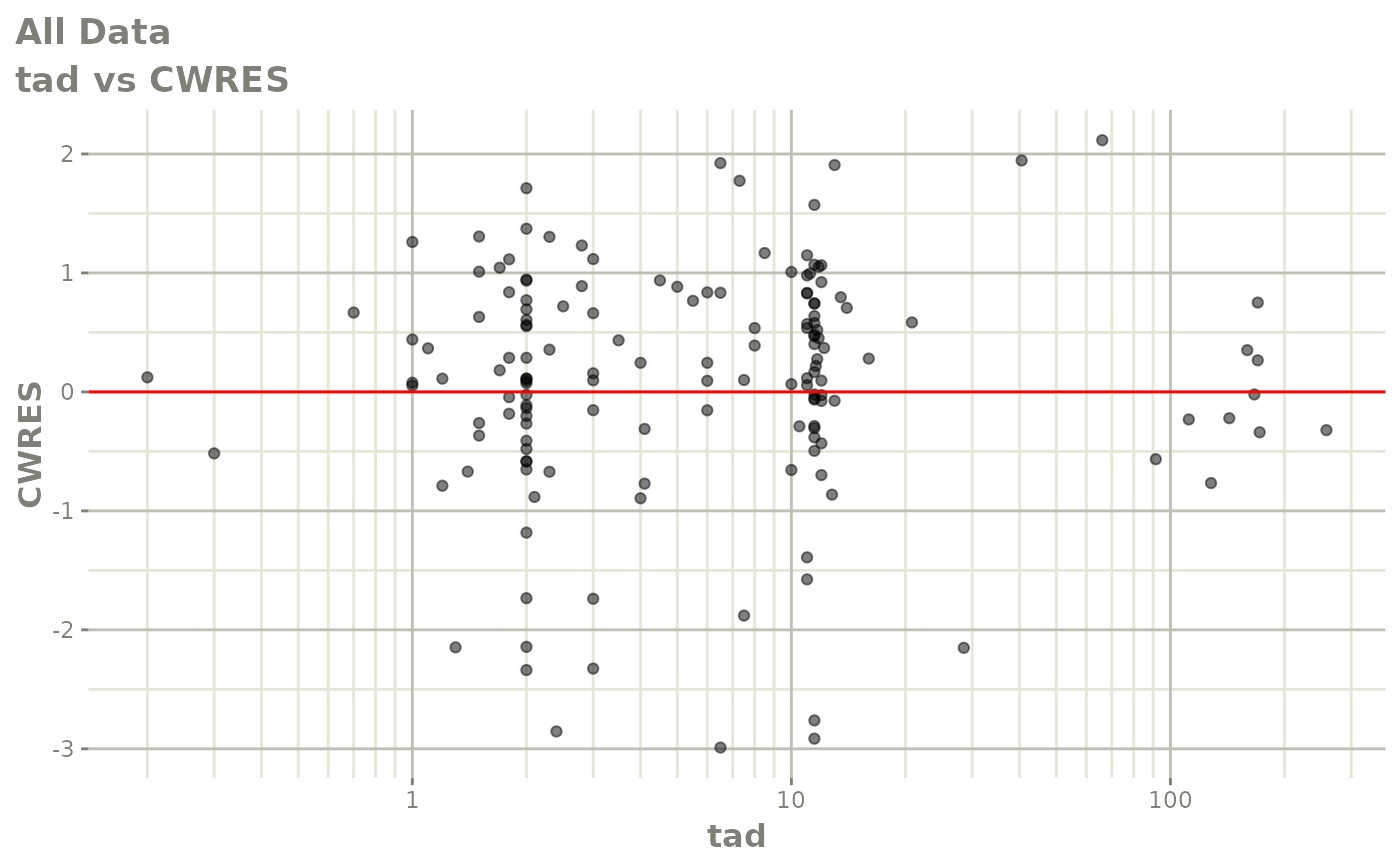
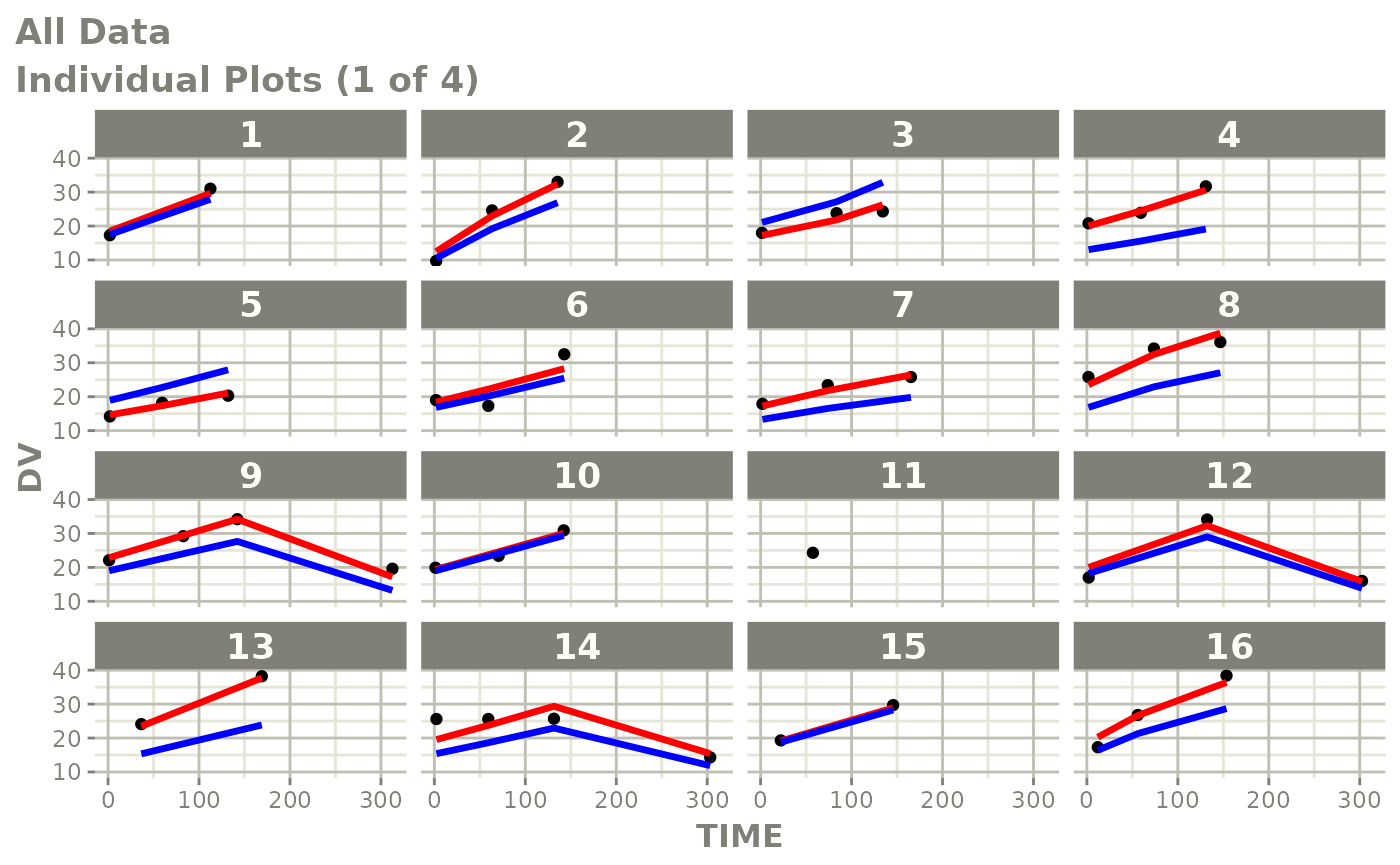
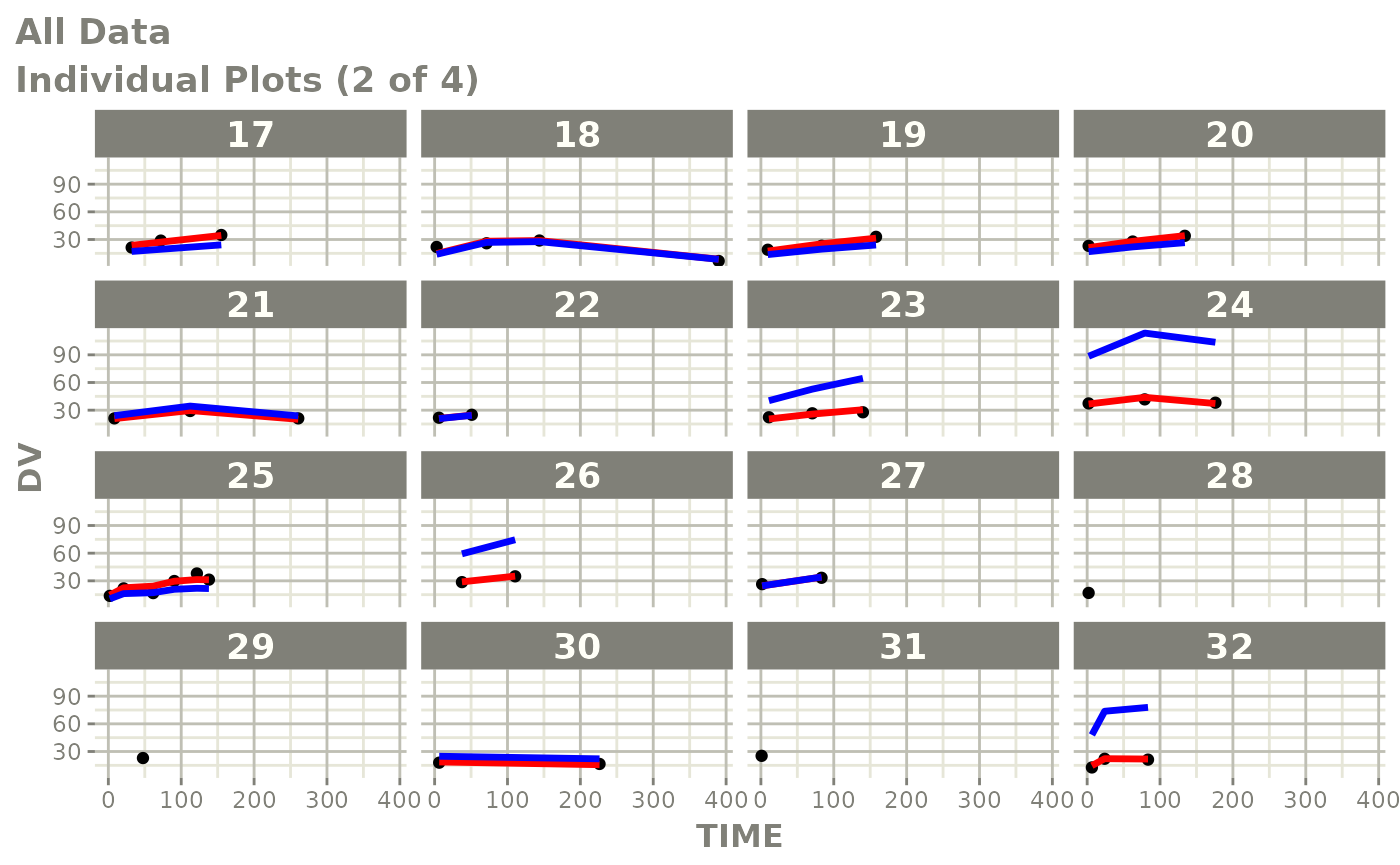
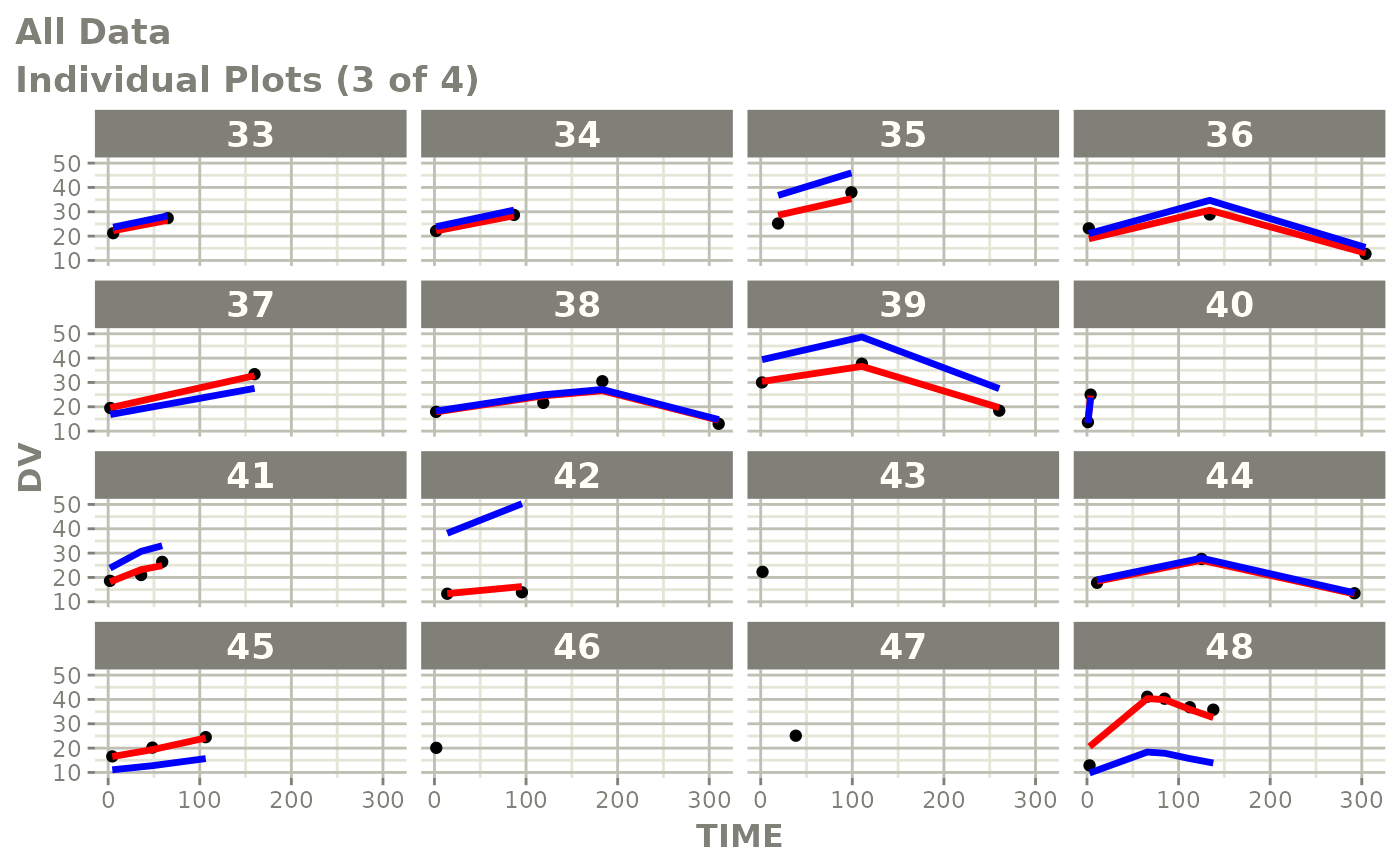
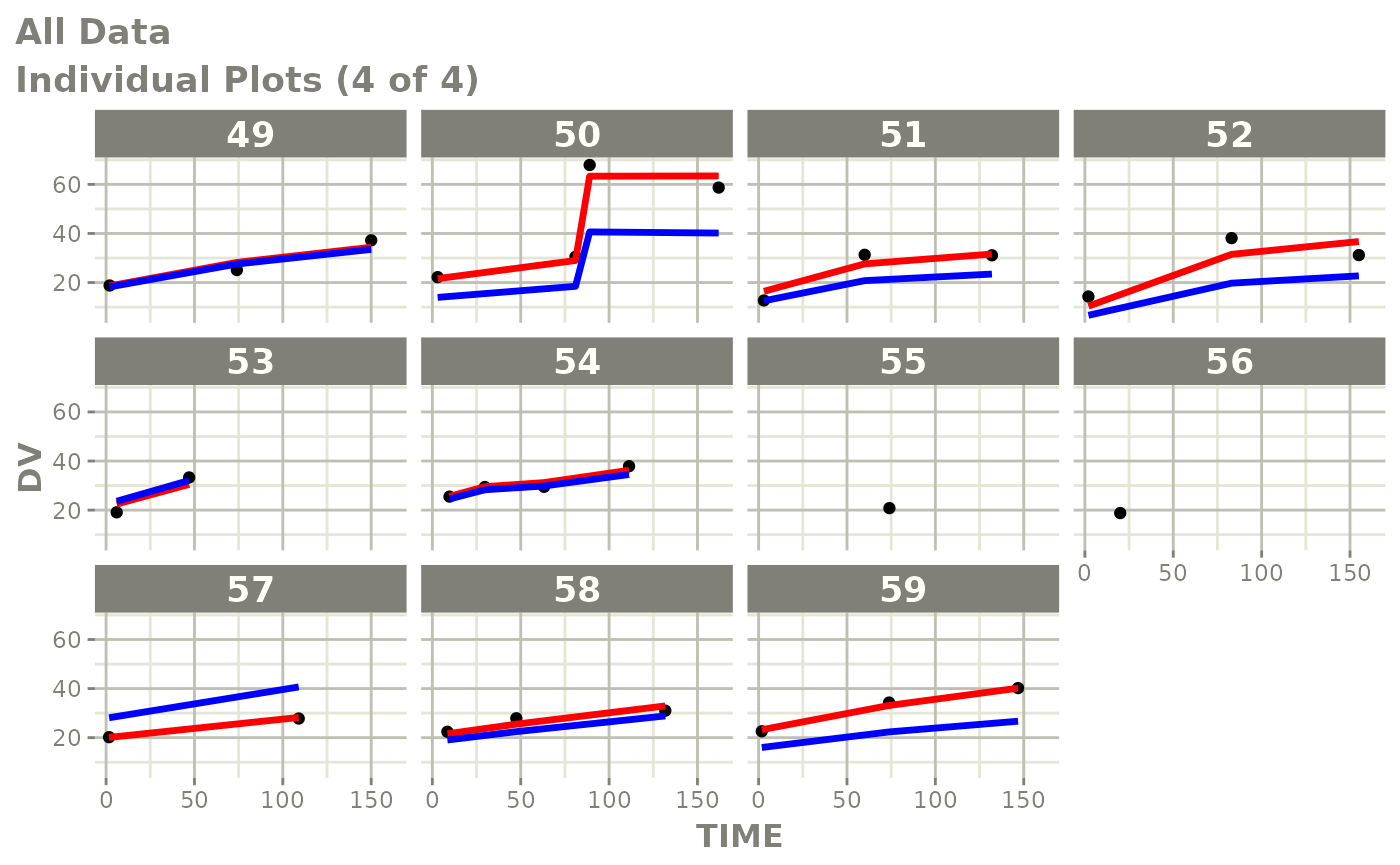
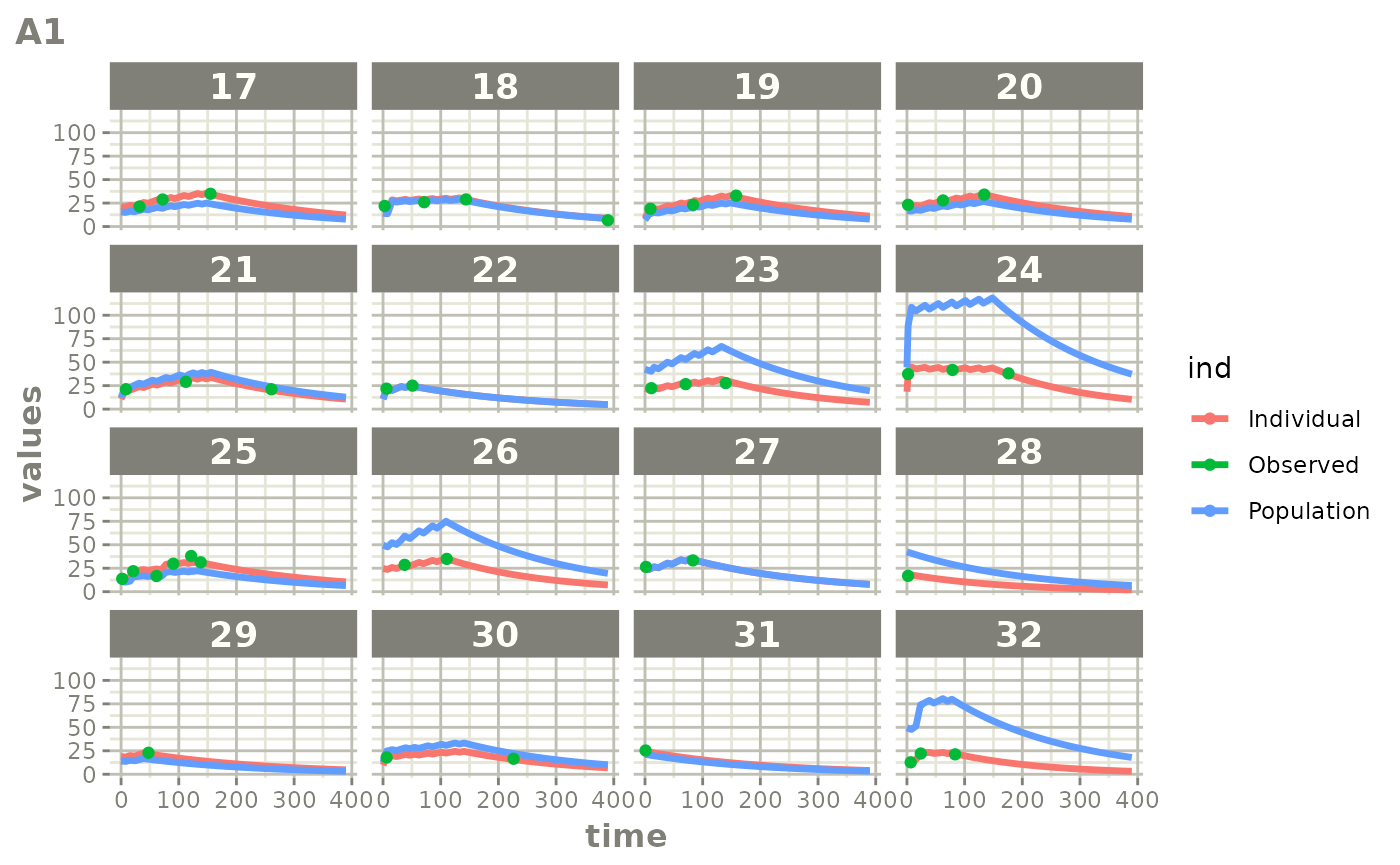
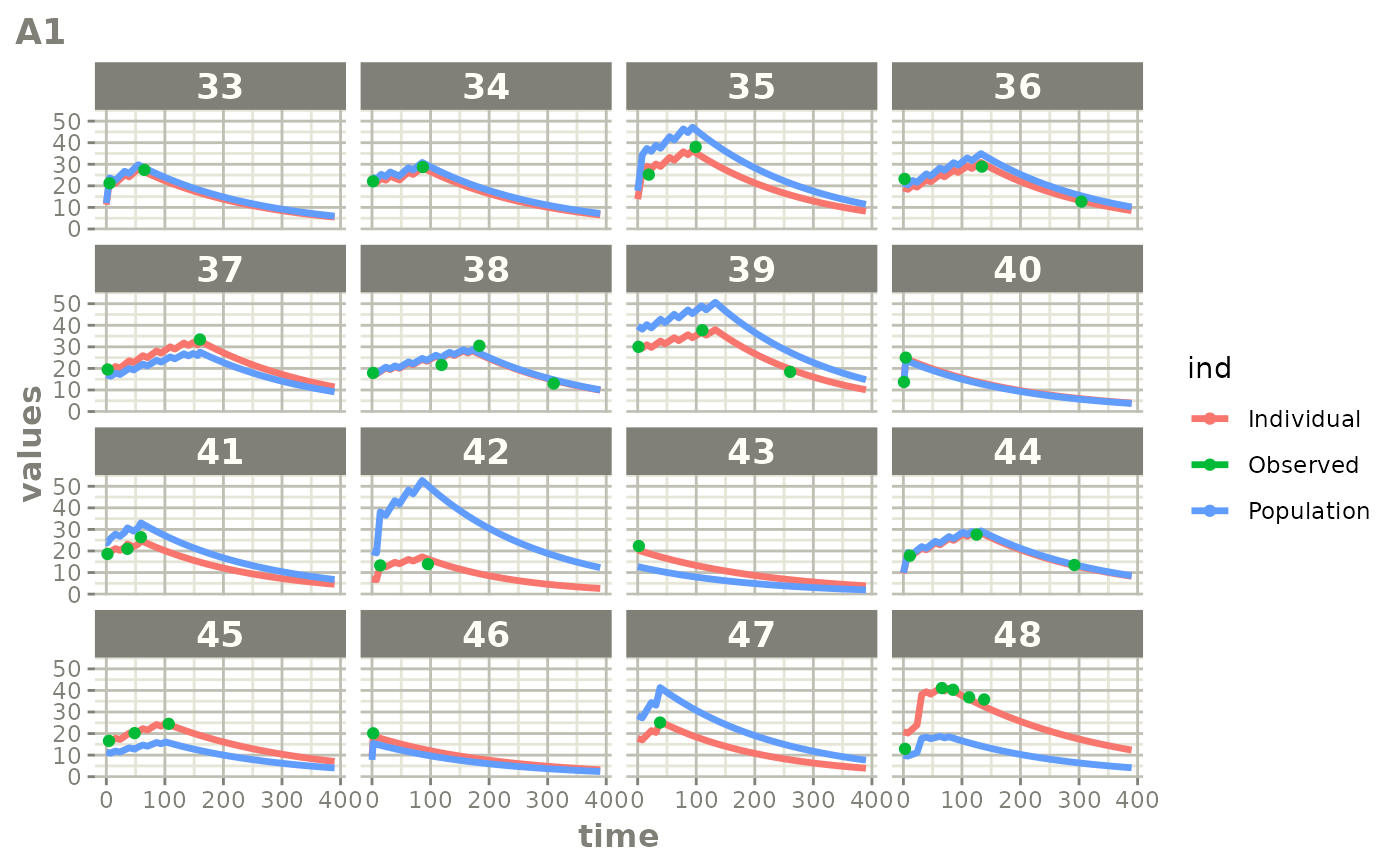
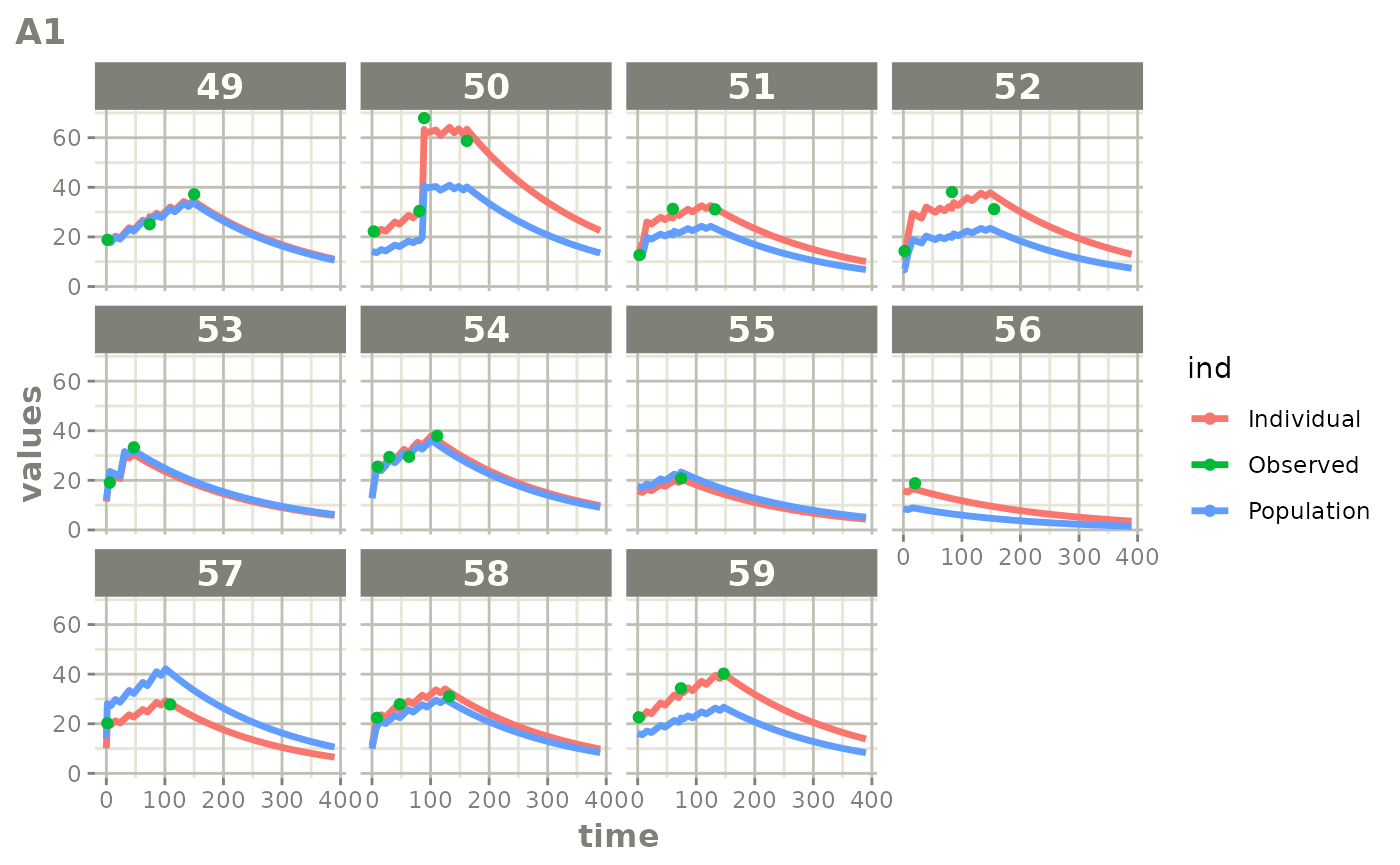
Those individual plots are not that great, it would be better to see the actual curves; You can with augPred

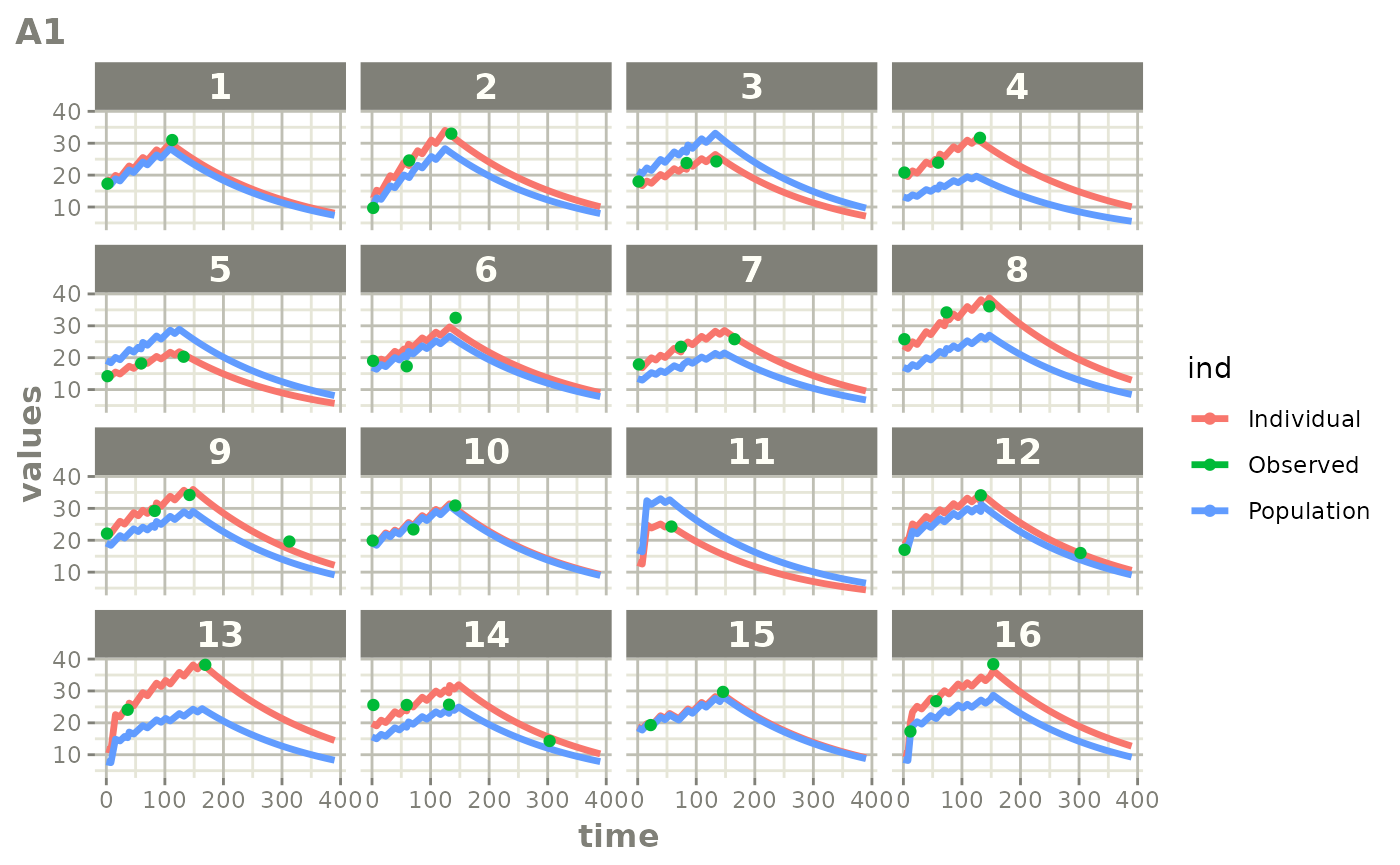
Two types of VPCs 

library(ggplot2)
p1 <- vpcPlot(fit, show=list(obs_dv=TRUE));
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
p1 <- p1 + ylab("Concentrations")

## A prediction-corrected VPC
p2 <- vpcPlot(fit, pred_corr = TRUE, show=list(obs_dv=TRUE))
#> [====|====|====|====|====|====|====|====|====|====] 0:00:00
p2 <- p2 + ylab("Prediction-Corrected Concentrations")

library(patchwork)
p1 / p2